Измерение размеров и контроль качества поверхностей деталей оптико-механическим способом, страница 4

                                                                      W_гр = 3n_гр − 2p₅ = 0,                                   (3)

где     W_гр - степень подвижности группы Ассура; n_гр - число звеньев в группе Ассура;

р₅ - число кинематических пар пятого класса в той же группе.

Выражение (3) справедливо, если число звеньев в группе Ассура будет чётным, а число кинематических пар пятого класса – кратным трём.

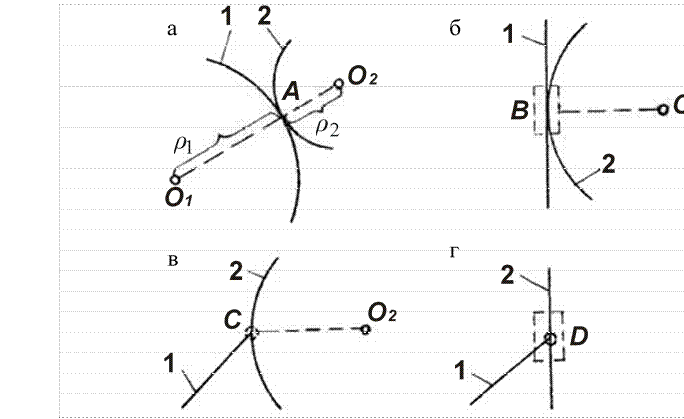
Рис. 6. Заменяющие кинематические цепи

При n = 2, p₅ = 3 образуется кинематическая цепь, удовлетворяющая условию (3), которая называется группой Ассура второго класса (рис. 7).

C

A

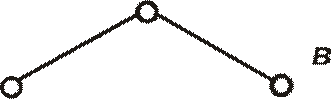
Рис. 7. Схематическое обозначение группы Ассура второго класса

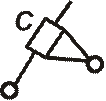
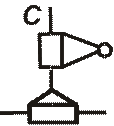
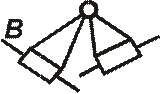
Группа Ассура второго класса может быть выполнена в пяти разновидностях (рис. 8), в зависимости от того, сколько вращательных пар и в каком порядке заменено парами поступательными. В группе следует различать внешние кинематические пары B и D (см. рис. 8), элементами которых она присоединяется к системе определённого движения (ведущим звеньям и стойке), и внутренние пары С, куда входят звенья самой группы.

Число внешних пар в группе определяет её порядок. На рис. 7 и 8 показаны группы Ассура второго порядка.

                            а C                    б C                   в

D

BD BB

                      г             C                              д B

D

D

Рис. 8. Виды групп Ассура второго класса: а - первый; б - второй; в - третий; г - четвёртый; д - пятый; B,C и D - кинематические пары пятого класса

При n = 4 (рис. 9) согласно уравнению (3) получим p₅ = 6. В этом случае ведомая часть механизма может состоять из следующих групп Ассура: а)  двух второго класса (рис. 9, а); б)  одной третьего класса (рис. 9, б); в)  одной четвёртого класса (рис. 9, в).

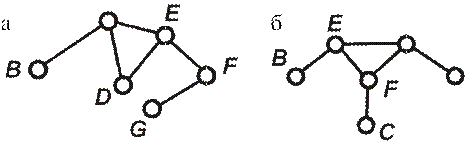C

G D

                                                                          в                   F

C

                                                                          B       D                                           

Рис. 9. Кинематические цепи с четырьмя звеньями: B,C,D,E,F,G – кинематические пары

Класс группы Ассура выше второго определяется числом пар основного замкнутого контура группы. На рис. 9, б это пары E,F и G, а на рис. 9, в – соответственно пары E,F,G и D. При числе звеньев в ведомой части механизма более четырёх, например равном шести, такая кинематическая цепь может оказаться состоящей их групп второго, третьего и четвёртого классов или образующей одну группу пятого класса и т.д.

Для определения класса механизма по Ассуру - Артоболевскому необходимо попытаться отделить от него группу второго класса (если это не удаётся, то группу более старшего класса) таким образом, чтобы после отделения осталась система определённого движения (т.е. оставшаяся часть также должна быть механизмом). Операцию разделения повторяют до тех пор, пока не останется одно ведущее звено со стойкой (механизм первого класса).

После разделения механизма на группы Ассура записывают формулу строения механизма и в соответствии с номером наивысшего класса присоединённой группы устанавливают класс механизма.

Примеры структурного анализа механизмов

Пример 1. Дан механизм (рис. 10). Определить его класс по Асуру - Артоболевскому. Решение

1.  Общее количество звеньев механизма k =12.

2.  Число подвижных звеньев n = k −1=11.

3.  Число пар пятого класса p₅ =16 (все пары вращательные).

4.  Количество пар четвёртого класса p₄ = 0. Необходимости в построении заменяющего механизма нет. Пассивные связи и звенья, вносящие лишние степени свободы, в механизме отсутствуют.

5.  Степень подвижности находим по формуле (2). 

                                           W = 3n − 2p₅ − p₄ = 3 11⋅ − 2 16⋅ − 0 =1.

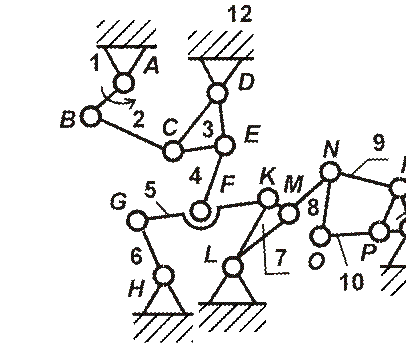
Рис. 10. Схема многозвенного механизма

Механизм имеет одно ведущее звено АВ.

Так как число ведущих звеньев совпадает со степенью подвижности механизма, ведущее звено входит в кинематическую пару со стойкой, и так как в механизме нет кинематических пар четвёртого класса, то можно приступить к разделению его на группы Ассура.