6. В данном случае отделить группу второго класса, отвечающую условию n = 2, p5 = 3, не разрушая оставшейся части (т. е. не нарушая определённости движения), не представляется возможным.
Поэтому отделяют группу MNOPRS, отвечающую условию n = 4, p5 = 6. В ней четыре внутренние пары, образующие основной замкнутый контур N,O,R и P, две внешние (M и S). Следовательно, отделена группа четвёртого класса второго порядка.
В оставшемся механизме ABCDEFKLHG можно отделить также только группу ELHGFK, удовлетворяющую условию n = 4, p5 = 6. Здесь три внутренние пары (G,F,K), образующие основной замкнутый контур, и три внешние (E,H,L). Поэтому отделена группа третьего класса третьего порядка.
Наконец, от оставшегося механизма ABCD отделяют группу BCD, удовлетворяющую условию n = 2, p5 = 3, т.е. группу второго класса второго порядка первого вида (рис. 8, а).
Данный механизм устроен следующим образом. К ведущему звену и стойке присоединена группа второго класса второго порядка первого вида, к ней и двум стойкам присоединена группа третьего класса третьего порядка, и к этой группе и стойке присоединена последняя группа четвёртого класса второго порядка.
Условно структуру механизма можно записать так:
1 (1; 2) 2(1)
(2; 3) 3(3) (4; 5; 6; 7) 
4(2)
(8; 9; 10; 11), где цифры обозначают: 1 - ведущее звено; 2 -
группу второго класса, а показатель – номер вида; 3 - группу третьего класса, а
показатель – номер порядка; 4 - группу четвёртого класса, а показатель – номер порядка.
Наивысшим классом присоединённой группы в данном случае оказался четвёртый, поэтому механизм, представленный на рис. 10, относится к четвёртому классу.
Если бы в состав механизма входили пары четвёртого класса, то предварительно перед разделением на группы следовало бы начертить схему заменяющего механизма, а затем поступить так, как было указано выше.
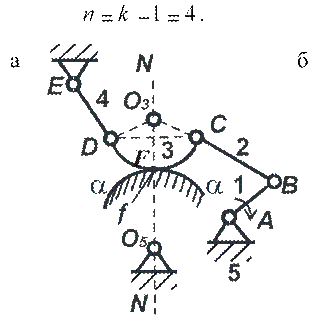
Пример 2. На рис. 11, а изображена схема механизма перекатывающихся рычагов. Определить его структуру и класс.
Решение
1. Число звеньев механизма k = 5.
2. Число подвижных звеньев
5
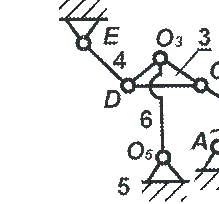
Рис. 11 Схема механизма перекатывающихся рычагов: а - до замены пары четвёртого класса F; б - после замены;
A,B,C,D,E,F - кинематические пары;
О3,О5 - центры кривизны профилей; 1-6 - звенья
3. Количество пар пятого класса p5 = 5 (пары A,B,C,D,E).
4. Количество пар четвёртого класса p4 =1 (пара F).
5. Степень подвижности
W = 3n − 2p5 − p4 = 3⋅4 − 2⋅5−1=1.
Ведущее звено должно быть одно, как и указано на схеме механизма; пассивных связей и звеньев, вносящих лишние степени свободы, нет.
6. Согласно рис. 6, а заменяем пару F четвёртого класса кинематической цепью, состоящей из одного звена и двух пар пятого класса (рис. 11, б). Для этого проводим в точке f (рис. 11, а) нормаль NN к профилям, образовавшим пару четвёртого класса, отмечаем на нормали центры O3 , O5 кривизны профилей и помещаем в них вращательные пары O3 , O5 .
Один из элементов пары О5 будет принадлежать звену O3 , O5 , а другой – звену, с которым был связан профиль αα. В данном случае это звено будет стойкой.
Один элемент пары О3 принадлежит звену О3,О5 , а другой – кривой DC, поэтому второй элемент данной пары (точка О3 ) жёстко связывается с точками D и C.
7. Как в примере 1, отделить группу второго класса, не разрушая оставшейся части механизма, невозможно. Поэтому приходится отделять группу, отвечающую условию n = 4, p5 = 6, т. е. отделять всю ведомую часть механизма.
В отделённой группе имеются три внутренние пары (C, О3 и D), образующие основной замкнутый контур, и три внешние пары (B, О5 и
E). Следовательно, эта группа относится к третьему классу и порядок её будет третий.
Условная запись механизма:
1 (1; 5) 
3(3)
(2; 3; 4; 6).
Таким образом, механизм (см. рис. 11) будет третьего класса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.