Измерение размеров и контроль качества поверхностей деталей оптико-механическим способом, страница 18

При большем числе опытов вычисление среднеарифметического значения случайной величины становится громоздким, поэтому их производят обычно приближённо, считая значение случайной величины x в пределах каждого из k интервалов (k < n) постоянным и равным среднему значению ^~x_i :

xi−1 − xi . x^%_i =

2

Тогда

k

                                                                                  .                                      (2)

i=1

Рассеивание размеров относительно среднего значения оценивается среднеквадратичным отклонением σ

σ=(3) или приближённо

σ=(4)

Чем больше σ, тем более разбросаны значения x вокруг среднеарифметического x.

Все расчёты при вычислении величин x и σ нужно выполнить в табличной форме (см. табл. 2).

Для большей наглядности полученные данные представляют в виде специального графика – гистограммы. Гистограмма строится следующим образом. По оси абсцисс в выбранном масштабе откладываются интервалы (рис. 4) и на каждом интервале, как на основании, строится прямоугольник, площадь которого в масштабе равна частности данного интервала. Высота такого прямоугольника h_i легко вычисляется по формуле

pi∗ h_i = .

xi − xi−1

В случае, если разряды равны, т. е. x₁ − x₀ = x₂ − x₁ =...= x_k − x_k−1, высоты прямоугольников пропорциональны соответствующим частностям p₁^∗, p₂^∗,..., p_k^∗. Совокупность всех построенных указанным способом прямоугольников и образует гистограмму.

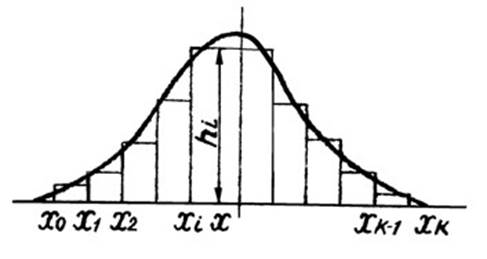
Рис. 4. Гистограмма

Считают, что случайные значения отклонений размера чаще всего подчиняются нормальному закону распределения

2

                                                                                         f x( ) =.                                          (5)

Подставив в уравнение (5) найденные ранее значения х и σ и задавая значения х х= _i (i =1,2,...), строим по точкам график этой функции в тех же координатах, что и гистограмму. Значения f (x_i ) откладываем по оси ординат в том же масштабе, что и h_i .

Сравнивая гистограмму с полученной кривой, можно определить, насколько близок полученный нами эмпирический закон распределения случайной величины x к теоретически точному.

Библиографический список

1.  Вентцель Е. С. Теория вероятностей. М.: Академия, 2003.

2.  Якушев А. И. Взаимозаменяемость, стандартизация и технические измерения. Машиностроение, 1986.

3.  Справочник конструктора точного приборостроения / Под ред. К. Н. Явленского. Л.: Машиностроение, 1989.

Лабораторная работа № 4

АТТЕСТАЦИЯ КАЛИБРА - ПРОБКИ С ПОМОЩЬЮ

ОПТИМЕТРА ИКГ

Цель работы: ознакомление студентов с конструкцией горизонтального оптиметра ИКГ, приёмами измерений на нём, определение отклонений от правильной геометрической формы детали и выдача на основании измерений заключения о годности измеряемой детали. Кроме этого, настоящая работа имеет своей целью также закрепление полученных на лекциях основных понятий об отечественной системе допусков на изготовление деталей и контрольных калибров.

Принцип действия и оптическая схема прибора

Оптиметр ИКГ представляет собой прибор с рычажно-оптической системой, предназначенной для измерения наружных и внутренних линейных размеров методом сравнения измеряемого изделия с концевыми мерами, калибрами или деталями-образцами.

Пределы измерения наружных размеров – от 0 до 350 мм, внутренних – от 13,5 до 150 мм. Цена деления шкалы – 0,001 мм. Рабочая область шкалы составляет ± 0,1 мм. Погрешность показаний при измерении наружных размеров составляет ± 0,0003 мм, а при измерении внутренних - ± 0,001 мм.

Конструктивная схема оптиметра базируется на принципе автоколлимации в сочетании с качающимся зеркальцем. В основу принципа автоколлимации положено свойство объектива превращать пучок лучей, исходящих из источника света, расположенного в фокусе объектива, в пучок параллельных лучей и затем собирать этот пучок, отражённый плоским зеркалом, в том же фокусе объектива.