Измерение размеров и контроль качества поверхностей деталей оптико-механическим способом, страница 17

б) положить на измерительный столик между подвижной и переставной пятками скобы измерительную плитку (концевую меру длины) так, чтобы она не касалась пяток; эта плитка нужна не как измерительный инструмент, а в качестве подставки под штифт для удобства измерения (см. рис. 3); в) пользуясь арретиром 6, положить на плитку между пятками скобы штифт так, чтобы поверхности штифта, ограничивающие проверяемый размер, касались пяток; г) отпустить арретир, снять отсчёт по шкале; если при небольших поворотах штифта стрелка будет показывать равные величины, то для штифтов с полукруглым торцом нужно найти наибольший отсчёт (см. рис. 3, а), а для штифтов с плоским торцом – наименьший (см. рис. 3, б). Если длина проверяемого штифта окажется больше или меньше предельных значений размера, которые можно измерить рычажной скобой при выбранной длине блока концевых мер, то такие штифты нужно отложить (отдельно бо́льшие и ме́ньшие). Измерение их следует выполнить после подбора для них соответствующего блока концевых мер. Результаты измерения занести в табл. 1.

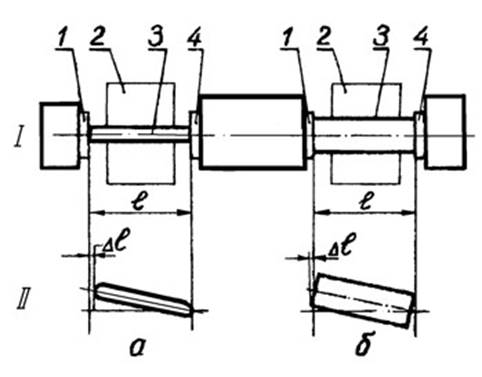
Рис. 3. Ошибки при измерении длины детали

Таблица 1

Результаты измерений

Такую таблицу обычно называют простой статистической совокупностью. Для получения достоверных значений статистических характеристик приходится проделать большое число замеров (n = 200, 300 и более). При таком числе наблюдений простая статистическая совокупность становится мало наглядной формой записи. Для придания полученным данным большей компактности и наглядности строится так называемый «статистический ряд».

В табл. 1 находят наибольшее ( x_max ) и наименьшее ( x_min ) отклонения размера от его номинального значения. Затем определяют величину зоны рассеивания действительного размера штифта

ν= xmax − xmin и разбивают всю зону на k интервалов. Практика расчётов показала, что удобнее всего применять k =10K20. Границы интервалов будем обозначать x₀ − x x₁; ₁ − x₂;...;x_k−1 − x_k.

Подсчитаем число m_i отклонений, укладывающихся в каждый интервал, и вычислим значение

                                                                                     *         mi

pi =   , n

которое называют «частностью» случайной величины для интервала xi−1 − xi .

Частность 0 ≤ p_i^∗ ≤1 показывает, как часто отклонение х размера

(случайная величина) попадает в соответствующий интервал. Рассматривая совокупность всех значений p i_i ( =1,2,...), можно сделать выводы о бо́льшей или ме́ньшей вероятности появления отклонения размера в тех или иных интервалах.

Полученные данные сводят в табл. 2.

В качестве одной из числовых характеристик статического материала выбирается среднеарифметическое отклонение

k

∑x_j

x = ^j=1       ,         (1) n

где      x_j - значение отклонения, полученное при j -измерении.

Таблица 2 Статистические параметры измерений

В различных партиях измеряемых штифтов значения x могут несколько различаться. Однако чем больше будет число измерений n, тем яснее проступит тенденция стремления x к некоторой постоянной величине. Величина, к которой приближается значение x при n → ∞, называется математическим ожиданием случайной величины x .