Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 9

Рассчитайте устойчивые оценки средних значений переменных по Винзору и Пуанкаре.

Решение. 1. Прежде всего проверим статистическую гипотезу о наличии грубых ошибок для переменной Х₁. Для этого следует ранжировать ее значения в порядке возрастания (убывания): 10,0   25,0   50,0   62,5   65,0   70,5   75,0   76,0   80,0   85,0   90,0   95,0.

Можно предположить, что значения 10,0 и 25,0 являются аномальными для данной совокупности. Проверим эти значения при помощи -критерия Титьена—Мура:

;                            

;                  

;                     

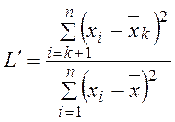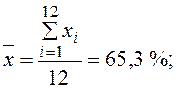
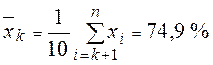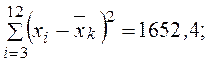
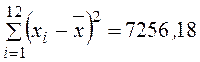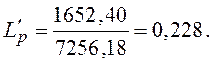
Табличное значение критерия равно 0,305. Так как , гипотеза подтверждается, следовательно, проверяемые значения 10,0 и 25,0 являются грубыми ошибками.

2. Для расчета устойчивых средних применим формулы Винзора и Пуанкаре:

а) средняя по Винзору

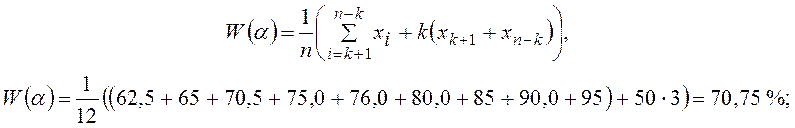
б) средняя по Пуанкаре

,

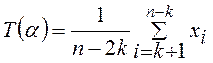n = 12, .

Параметр  a  определяем по специальной таблице (приложение) в зависимости от степени «засоренности» выборки

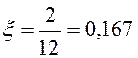;      a » 0,164;   k £ 0,164×12 = 2,004;      k = 2

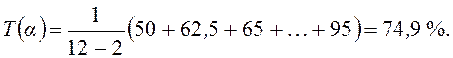
Аналогичные расчеты выполните самостоятельно для переменной Х₂ (рентабельность производства).

Пример 2.    Имеются следующие данные о ежедневных объемах  реализации продукции по 20 предприятиям розничной торговли за месяц (табл. 2.2).

Таблица 2.2

Номер предприятия	Реализовано, тыс. ден. ед.	Номер предприятия	Реализовано, тыс. ден. ед.
1	450	11	790
2	520	12	600
3	537	13	450
4	480	14	550
5	560	15	640
6	600	16	800
7	310	17	635
8	250	18	450
9	900	19	700
10	850	20	1200

1.  При помощи критерия Граббса проверьте, являются ли значения 250 и 1200 грубыми ошибками.

2.  Используя метод Хубера, проведите несколько итераций по расчету устойчивой оценки средней.

Решение. Прежде всего для рассматриваемой совокупности исчислим среднее значение признака и среднее квадратическое отклонение.

Расчетное значение Т-критерия Граббса для проверяемого значения признака 250 и уровня значимости α = 0,05 равно

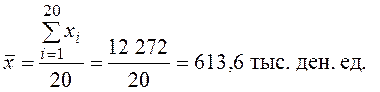
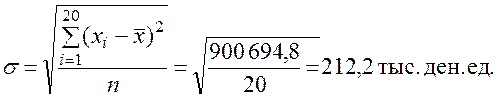
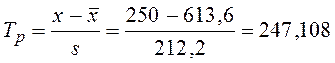, табличное значение Т_кр = 2,779.  Поскольку Т_р > Т_кр, проверяемое значение признака 250 является грубой ошибкой, т.е. аномальным наблюдением.

Аналогичные расчеты выполним и для максимального значения 1200

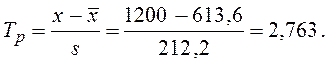
В этом случае Т_р < Т_кр, следовательно, проверяемое значение 1200 не является грубой ошибкой для данной совокупности.

1.  Используя метод Хубера, рассчитаем устойчивую оценку средней. Для первой итерации в качестве оценки величины θ возьмем среднюю .

В нашем примере число подозреваемых грубых ошибок равно единице, значит ξ = 1/20 = 0,05. По таблице  (см. параграф 2.4) находим k(ξ) = 1,399.

Разобьем всю совокупность на три класса (табл. 2.3).

Таблица 2.3

Значения переменных	І класс	ІІ класс	ІІІ класс
	613,6 - 1,399 < xi< 613,6 + + 1,399 612,2 < xi < 615	612,2 < xi	xi < 615
Исходные		900  850  790 640  800  635 700  1200	450  520  537 480  560  600  310 250  600    450     550  450
Модифицированные		898,6  848,6  788,6  638,6  798,6  633,6  698,6  1198,6	451,4  521,4  538,4  481,4  561,4  601,4  311,4  251,4  601,4  451,4    551,4    451,4