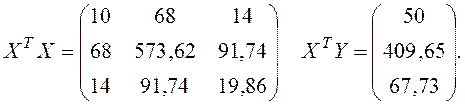
Рассчитываем элементы обратной матрицы ![]() и вектор оценок коэффициентов
регрессии A. Определитель матрицы
и вектор оценок коэффициентов
регрессии A. Определитель матрицы ![]() , а обратная матрица
, а обратная матрица ![]() равна
равна
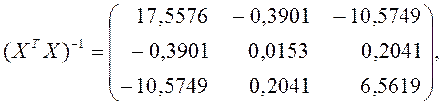
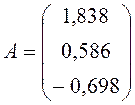
и оценку уравнения регрессии ![]() . Получаем
. Получаем
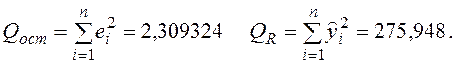
Тогда несмещенная оценка остаточной дисперсии равна
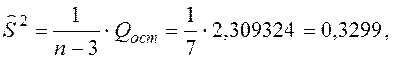
а оценка среднеквадратического отклонения составит ![]()
Проверяем на уровне значимости ![]() адекватность уравнения
регрессии, т.е. гипотезу
адекватность уравнения
регрессии, т.е. гипотезу ![]() . Для
этого вычисляем наблюдаемое значение F-критерия
. Для
этого вычисляем наблюдаемое значение F-критерия
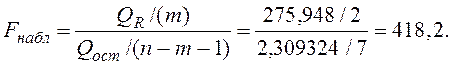
По таблице F-распределения для заданного уровня значимости
α = 0,05 и числа степеней свободы v1 = 3 и
v2 = 7
находим ![]() .
.
Так как ![]() ,
гипотеза отвергается с вероятностью ошибки 0,05. Таким образом, уравнение
является значимым, т.е. хотя бы один из рассчитанных коэффициентов регрессии
отличен от нуля.
,
гипотеза отвергается с вероятностью ошибки 0,05. Таким образом, уравнение
является значимым, т.е. хотя бы один из рассчитанных коэффициентов регрессии
отличен от нуля.
Перед проверкой значимости отдельных коэффициентов регрессии найдем оценку ковариационной матрицы вектора коэффициентов регрессии (A):
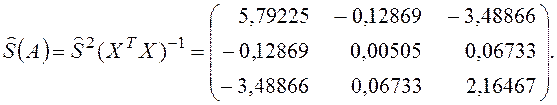
Учитывая, что на главной диагонали ковариационной матрицы находятся дисперсии коэффициентов регрессии, получаем следующие несмещенные оценки этих дисперсий:
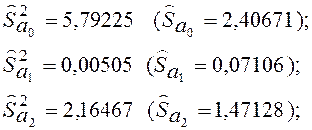
и оценку корреляционной матрицы Ra с элементами, определяемыми по формуле
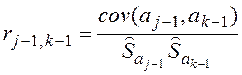 , где
, где ![]() —
элементы матрицы
—
элементы матрицы ![]() , стоящие на
пересечении j-строки и k-столбца, j, k = 1,2,3.
, стоящие на
пересечении j-строки и k-столбца, j, k = 1,2,3.
Находим оценку корреляционной матрицы Ra
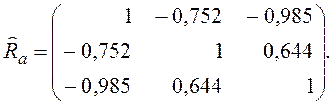
Для проверки значимости отдельных коэффициентов
регрессии, т.е. гипотез ![]() ,
где m=
0,1,2 находим по таблицам F-распределения для
,
где m=
0,1,2 находим по таблицам F-распределения для ![]() критическое значение
критическое значение ![]()
Вычисляем ![]() для
каждого из коэффициентов регрессии по формуле
для
каждого из коэффициентов регрессии по формуле
![]() Подставляя данные, получаем
Подставляя данные, получаем
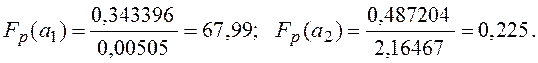
Так как ![]() , то
коэффициент регрессии
, то
коэффициент регрессии ![]() значимо отличается
от нуля. Для коэффициента
значимо отличается
от нуля. Для коэффициента ![]() выполняется
неравенство
выполняется
неравенство ![]() , поэтому данный
коэффициент можно считать незначимым.
, поэтому данный
коэффициент можно считать незначимым.
Таблица 3.5
|
Номер предприятия |
Х1 |
Х2 |
Х3 |
Номер предприятия |
Х1 |
Х2 |
Х3 |
|
1 |
240 |
8 |
37 |
16 |
236 |
5 |
21 |
|
2 |
280 |
10 |
33 |
17 |
300 |
10 |
40 |
|
3 |
265 |
15 |
28 |
18 |
248 |
6 |
31 |
Окончание табл. 3.5
|
Номер предприятия |
Х1 |
Х2 |
Х3 |
Номер предприятия |
Х1 |
Х2 |
Х3 |
|
4 |
350 |
4 |
45 |
19 |
214 |
8 |
28 |
|
5 |
295 |
12 |
29 |
20 |
280 |
2 |
30 |
|
6 |
270 |
10 |
38 |
21 |
165 |
4 |
15 |
|
7 |
180 |
5 |
24 |
22 |
180 |
2 |
17 |
|
8 |
250 |
7 |
28 |
23 |
315 |
20 |
45 |
|
9 |
310 |
12 |
34 |
24 |
200 |
7 |
20 |
|
10 |
345 |
15 |
38 |
25 |
274 |
11 |
37 |
|
11 |
220 |
6 |
26 |
26 |
194 |
5 |
25 |
|
12 |
180 |
3 |
18 |
27 |
267 |
18 |
32 |
|
13 |
175 |
3 |
20 |
28 |
280 |
10 |
45 |
|
14 |
190 |
6 |
21 |
29 |
320 |
12 |
50 |
|
15 |
215 |
3 |
29 |
30 |
380 |
18 |
55 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.