Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 14

Обычно предполагается, что случайная величина (Y) имеет нормальный закон распределения с условным математическим ожиданием  и постоянной, не зависящей от аргументов дисперсией .

В анализе чаще всего используются уравнения регрессии линейного вида

.

Коэффициенты регрессии  показывают, на какую величину в среднем изменяется результативный признак Y, если независимая переменная изменяется на единицу ее измерения.

В матричной форме регрессионная модель имеет вид

, где Y — случайный вектор-столбец размерности  наблюдаемых значений результативного признака ; Х — матрица размерности  наблюдаемых значений аргументов. Элемент матрицы  рассматривается как неслучайная величина (i= 1, 2,…n;  j= 0, 1, 2,…m; );  — вектор-столбец размерности  неизвестных параметров, подлежащих оценке в ходе регрессионного анализа (вектор коэффициентов регрессии);  — случайный вектор-столбец размерности  — вектор остатков, которые являются независимыми нормально распределенными случайными величинами с нулевым математическим ожиданием () и неизвестной дисперсией . На практике рекомендуется, чтобы число наблюдений (n)  превышало число анализируемых признаков  (m) не менее, чем в пять-шесть раз.

Для расчета вектора оценок коэффициентов регрессии А = (a₀, a₁,…a_m) по методу наименьших квадратов используется формула

,                                                (3.4)

где

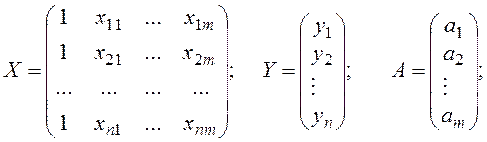
 — транспонированная матрица Х;  — матрица, обратная матрице .

Для устранения влияния различия дисперсий и единиц измерения отдельных переменных на результаты регрессионного анализа в ряде случаев целесообразно вместо исходных значений переменных  использовать стандартизованные значения  z_ij =(x_ij –x_j)/σ_j. В этом случае уравнение множественной линейной регрессии будет иметь следующий вид:

                               (3.5)

где   — стандартизованные значения отклика  Y; Z_j  — стандартизованные значения предикторов (независимых переменных — X_j); β_j — стандартизованные коэффициенты регрессии, которые могут быть вычислены исходя из следующей системы уравнений:

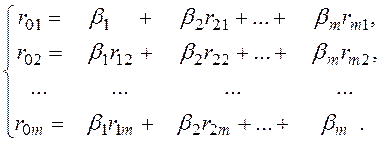
Если решать данную систему по правилу Крамера, то β_jравно

β_j =|R_j|/|R|,                                                   (3.6)

где  |R| — определитель матрицы системы уравнений; |R_j| — определитель матрицы системы линейных уравнений, в которой  j-й столбец заменен столбцом свободных членов уравнений системы (r₀₁, r₀₂ ,…r_0m).

Когда уравнение построено в стандартизованном масштабе, коэффициенты регрессии  β₁ , β₂, …β_m  показывают, на сколько стандартных отклонений изменится  Yпри изменении каждой из X_j  на одно стандартное отклонение. Между коэффициентами  а_j  и  β_j  существует следующая зависимость:

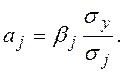                                                   (3.7)

Кроме того, при помощи коэффициентов  β_j   можно рассчитать частные (r²_ij) и множественный (R²_0/1,2, …_m) коэффициенты детерминации

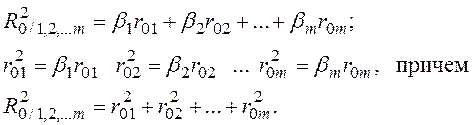
После того как рассчитано само уравнение регрессии и перечисленные выше характеристики корреляционных связей, необходимо убедиться в адекватности полученных результатов.

Значимость уравнения регрессии в целом, т.е. нулевая гипотеза , проверяется по F-критерию Фишера. Его наблюдаемое значение определяется по формуле

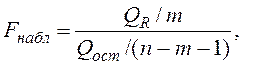                                    (3.8)

где .

По таблице распределения значений F-критерия Фишера, при заданных , находят . Гипотеза  отклоняется с вероятностью , если  . Из этого следует, что уравнение является значимым, т.е.  хотя бы один из коэффициентов регрессии существенно отличен от нуля.

Для проверки значимости отдельных коэффициентов регрессии, т.е. гипотез , где j= 1,2,…,m, используют t-критерий Стьюдента, фактическое значение которого вычисляют следующим образом:

   (3.9)

где  Ŝ²_aj  —  средняя ошибка коэффициента регрессии  a_j; Ŝ²_ост — оценка среднего квадрата ошибки; с_jj — соответствующие коэффициенту a_j  диагональные элементы матрицы  (X^TX)^–1.