Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 4

Следовательно, нулевая гипотеза о равенстве векторов средних значений двух множеств принимается, т.е. расхождения между работающими мужчинами и женщинами по изучаемым признакам несущественные.

1.1.3. Проверка гипотезы о равенстве ковариационных матриц

Сравнение ковариационных матриц, отражающих взаимосвязи изучаемых признаков, открывает возможность дополнить и уточнить гипотетические предположения относительно самих признаков. Это имеет особое  значение, если принять во  внимание, что даже специфические, индивидуальные признаковые характеристики могут совпадать случайно.

В социальных и экономических исследованиях существует множество задач, требующих идентификации признаковых связей. Особенно часто они возникают при  классификации  наблюдаемых  объектов, распознавании образов и т.п. Например, при оценке кредитоспособности клиентов банков, при группировке предприятий по уровню устойчивости финансового положения или при оценке эффективности  производственной и коммерческой деятельности.

Решения многомерными методами статистики большинства задач изначально предполагают равенство ковариационных матриц различных выборочных совокупностей. Например, в дискриминантном анализе рассматриваются две генеральные совокупности, имеющие многомерный нормальный закон распределения и равные ковариационные матрицы.

На практике учет ковариаций изучаемого комплекса признаков и проверка равенства ковариационных матриц значительно снижает вероятность появления ошибки в выводах. Это происходит из-за весьма малой вероятности случайного совпадения одновременно большого числа сложных характеристик признаковых связей.

Для одномерных случайных величин проверка гипотезы о равенстве их дисперсий в разных выборочных совокупностях осуществляется при помощи критерия Бартлетта

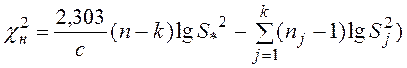,                            (1.5)

при 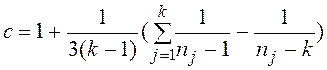  , где k — число нормально распределенных выборочных совокупностей; n_j — объемы каждой из  k-выборок, ; n — общий объем  всех  выборочных  совокупностей ;  — дисперсия признака в j-й выборочной совокупности,  ;  — объединенная  (средняя)  по  выборкам  дисперсия, где .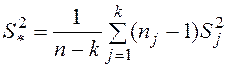

Для  c²-статистики критические значения находят по  таблицам квантилей  c²-распределения по заданному уровню значимости  (a)  и числу степеней свободы v = k-1. Нулевая гипотеза  о  равенстве дисперсий отклоняется, если   и  принимается, когда  .

В многомерном анализе сравниваются не дисперсии, а ковариационные матрицы двух  m-мерных выборочных совокупностей. Критерий принимает следующий вид:

,                                                  (1.6)

где параметры  b  и   –2ln v₁ определяются по следующим формулам:

                               (1.7)

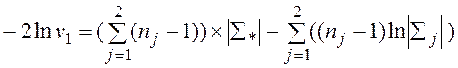,                             (1.8)

где m — число признаков, представляющих многомерную выборочную совокупность.

Величина  многомерного  ω-критерия сравнивается с   — табличными значениями и степенями свободы .

Пример 4. На основе данных из примера 2 произведем расчет ω-критерия по рассчитанным ранее ковариационным матрицам для каждой выборки

 ; 

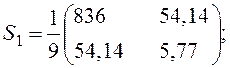
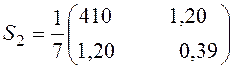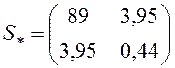
и  n₁ = 9;  n₂ = 7;  ;  ;       

Предварительно рассчитаем значения величин  b  и  –2 ln n₁:

;

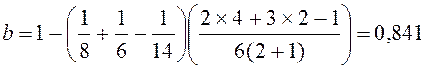Расчетное значение ω-критерия равно .

Критическое значение ω-критерия найдем по таблицам c²-распределения при  a = 0,05  и числе степеней свободы  m(m + 1)/2  или

=(2×3)/2 = 3; .

Так как  , следует отвергнуть нулевую гипотезу о равенстве ковариационных матриц S₁  и  S₂. То есть при заданном уровне значимости  a = 0,05  их  различие существенно.

Следовательно, вариация и ковариация признаков в рассматриваемых выборках существенно отличаются, при том, что гипотеза о равенстве векторов средних значений подтвердилась (см. предыдущий пример).

1.2.  Контрольные задания

Задание 1. В табл. 1.5 приведены результаты статистического наблюдения, проводимого на предприятиях, входящих в состав концерна.

Таблица 1.5