Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 24

Здесь: Х₁ — прибыль от реализации продукции, тыс. ден. ед.; Х₂ — объем реализованной продукции, тыс. ден. ед.; Х₃ — запасы товарно-материальных ценностей на конец года, тыс. ден. ед.; Х₄ — средства, используемые на развитие производства, тыс. ден. ед.

Рассчитайте значение  F-критерия при a = 0,05 и с его помощью оцените значимость уравнения регрессии и множественного коэффициента корреляции. Проанализируйте полученные результаты и сделайте выводы.

Задание 3. По данным табл. 3.9 об уровне цен импорта отдельных продуктов за ряд лет постройте матрицу парных корреляций (R). Оцените существующие взаимосвязи между уровнями цен на различные виды импортной продукции. Рассчитайте линейную регрессионную модель зависимости уровня цен одной тонны пшеницы от уровня цен на другие виды импортной продукции.

Оцените значимость регрессионной модели и матрицы парных корреляций при помощи статистических критериев.

Таблица 3.9

Все необходимые расчеты выполните на компьютере с использованием специального пакета прикладных программ STATISTICA. Протоколы работы соответствующих модулей распечатайте и поясните полученные результаты.

Задание 4. В ходе проведения множественного корреляционно-регрессионного анализа была получена система линейных уравнений относительно стандартизованных коэффициентов регрессии β_j

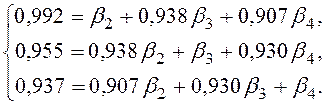
1. Рассчитайте значения стандартизированных коэффициентов β_j и постройте уравнение регрессии для зависимой переменной  X₁  в стандартизованном масштабе.

2. В матричной форме рассчитайте множественные коэффициенты детерминации и корреляции, поясните полученные результаты.

Задание 5. На основании данных выборочной совокупности  (n = 30) была рассчитана матрица парных корреляций

.

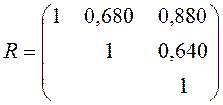1. Учитывая, что зависимой переменной (откликом) является переменная X₁,  а  независимыми переменными (предикторами) — X₂  иX₃, рассчитайте множественные коэффициенты детерминации и корреляции.

2. На основании критерия Снедекора оцените значимость множественного коэффициента детерминации при уровне значимости α = 0,01.

3. Постройте уравнение множественной регрессии в стандартизированном масштабе и поясните смысл его параметров.

Задание 6. В результате проведения регрессионного анализа по 50 наблюдениям построена регрессионная модель

где  Y —  индекс физического объема ВВП, %; X₁ — индекс объема продукции промышленности, %; X₂ — индекс объема продукции сельского хозяйства, %; X₃ — индекс объема внешнеторгового оборота, %.

Множественный коэффициент детерминации R² = 0,562.

Наблюдаемые значения  t-критерия Стьюдента для коэффициентов регрессии равны для:      a₁ = -0,004;          t_р= -0,136;

a₂ = 0,182;             t_р= 1,674;

a₃ = 0,203;             t_р = 3,830.

1. Проверьте достоверность полученной регрессионной модели в целом и отдельных ее коэффициентов.

2. Оцените степень тесноты связи между динамикой ВВП и рассматриваемыми факторами. Поясните полученные результаты.