Проведите корреляционно-регрессионный анализ взаимосвязи приведенных признаков с использованием пакета STATISTICA. Распечатайте и поясните полученные результаты.
При помощи t-критерия Стьюдента и F-критерия Фишера оцените значимость показателей тесноты связи и адекватность уравнения регрессии. При помощи частных коэффициентов детерминации оцените информативность отдельных факторных признаков с точки зрения их влияния на результативную переменную.
Решение. После ввода исходных значений анализируемых переменных в стартовой панели анализа данных выбираем модуль «Линейная регрессия» (Linearregression). В открывшемся окне (рис. 3.1) указываем зависимую (Dependent) и независимые переменные (Independent). Нажимаем ОК.
В качестве зависимой переменной в данном примере будет выступать величина средней заработной платы (X1), а две других переменных (X2, X3) выступают в качестве факторов. После выбора переменных, участвующих в анализе, на экране появляется окно с предварительными результатами и предлагаемым набором функций для дальнейшего анализа.
В диалоговом окне (рис. 3.2) содержатся начальные результаты работы модуля «Множественная регрессия» (MultipleRegression):
Dep. Var — зависимая переменная Y; Multiple R — множественный коэффициент корреляции, R = 0,896; Standarderrorofestimate — стандартная ошибка аппроксимации равна 26,7 %.
Кроме того, в окне указан свободный член уравнения и его стандартная ошибка: Intercept — свободный член уравнения равен 99,17; Std. Error — стандартная ошибка свободного члена равна 16,09 %;
F-критерий Фишера равен 55 при числе степеней свободы в числителе 2, а в знаменателе 27; расчетное значение t-критерия для оценки значимости свободного члена равно 6,16.
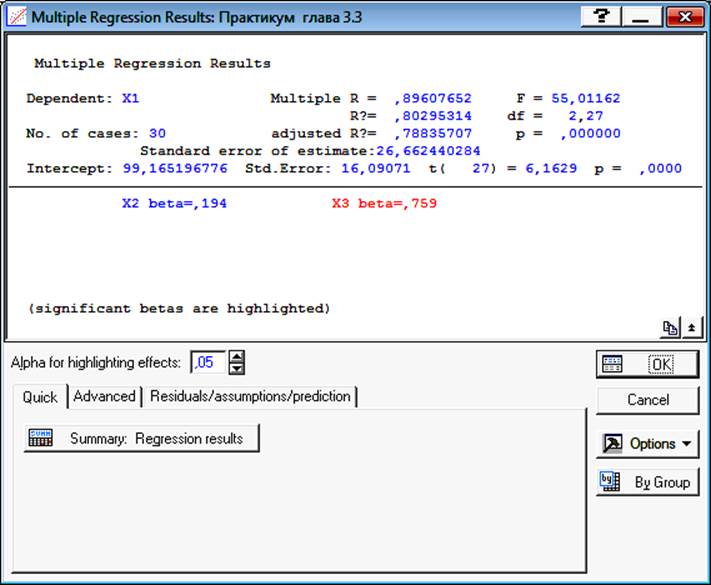
На рис. 3.3 даны также результаты дисперсионного анализа (факторная и остаточная дисперсия, а также расчетное значение F-критерия Фишера). Судя по критерию Фишера (Fрасч.= 55,0 > Fтабл.= 3,369), уравнение регрессии в целом следует признать адекватным.
Множественный коэффициент детерминации R2 = 0,896 можно разложить на частные коэффициенты детерминации. Для этого найдем попарные произведения β-коэффициентов на соответствующие парные коэффициенты корреляции факторов с результативной переменной. Рассчитать эти коэффициенты можно при помощи модуля BasicStatisticsandTablesвторая функция Correlationmatrices).
Рисунок 3. 4 Окномодуля Basic Statistics and Tables
Рисунок 3. 5 Выбор переменных для построения корреляционной матрицы

Рисунок 3.6 Матрица парных коэффициентов корреляции
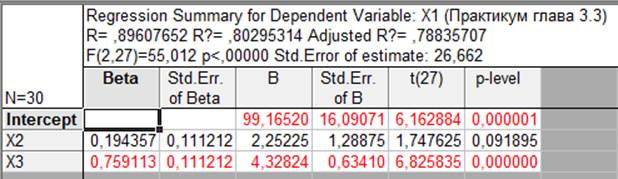
Первый частный коэффициент детерминации равен 0,132 (0,194×0,68), а второй — 0,668 (0,759×0,88). Проверим правильность расчетов: 0,132 + 0,668 = 0,800, а множественный коэффициент детерминации равен R2 = 0,803. Небольшое расхождение возникает за счет округления. Следовательно, на долю первого фактора приходится приблизительно 13,2 % объясненной дисперсии, а на долю второго фактора — 66,8 %. На основании этого, можно сделать вывод, что в данном случае вариация средней заработной платы в основном определяется вариацией производительности труда и слабо зависит от вариации стажа работы.
Для того чтобы продолжить регрессионный анализ, нажмем в левом верхнем углу активного окна кнопку Continue, вернемся в предыдущее окно (см. рис. 3.2) и выберем функцию Residual analysis — анализ остатков. На экране появится окно, содержащее шесть групп процедур для анализа остатков (рис. 3.7). Рассмотрим некоторые из них.
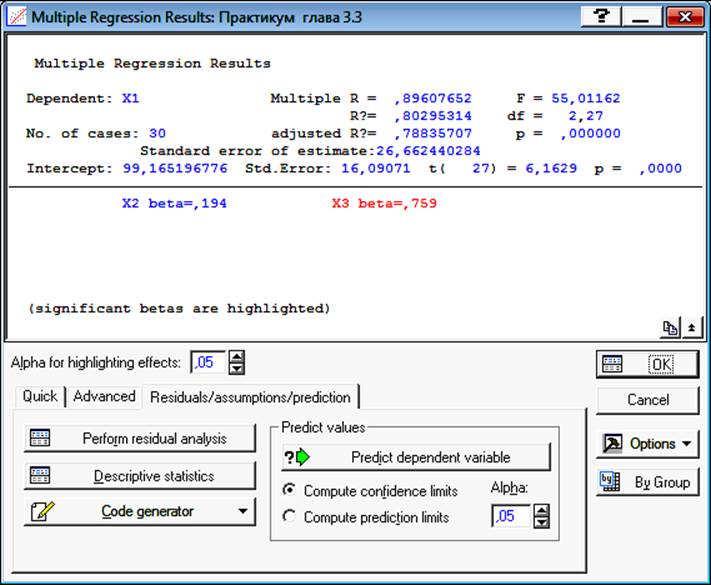
Рис. 3.7. Процедуры, предлагаемые для анализа остатков
Для примера рассмотрим процедуру Prediceted and residuals (рис. 3.8). В раскрывшемся окне появится таблица, содержащая исходные значения зависимой переменной и значения этой переменной, полученные на основе уравнения регрессии (рис. 3.8):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.