Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 21

Окончание табл. 3.6

Здесь: Х₁ — уровень рентабельности производства, %; Х₂ — удельный вес рабочих в составе работающих; Х₃ — размер премий и вознаграждений на одного работника, тыс. ден. ед.; Х₄ — уровень фондоотдачи, ден. ед.; Х₅ — оборачиваемость нормируемых оборотных средств, дней.

Решение. 1. Введем в таблицу исходные значения переменных и сохраним их в виде файла с именем  PRAKT2. На главной панели инструментов щелкаем по кнопке Analysisи в раскрывшемся окне выбираем StatupPanel модуль BasicStatistics процедуру Correlationmatricesи щелкаем  по  кнопке OK.

В раскрывшемся окне (рис. 3.8) указываем, для каких переменных должна быть построена матрица корреляций, выбираем и щелкаем на кнопке Correlations. На экране появится окно с матрицей парных корреляций, позволяющей судить о тесноте  линейной корреляционной связи между признаками.

Как видно из этой матрицы, самая тесная прямая связь с результативной переменной у фактора X₃ (r₁₃ = 0,52), а самая слабая связь у фактора X₂ (r₁₂ = 0,29). Следует обратить внимание на тот факт, что между факторными переменными  X₂  и  X₅  существует достаточно тесная связь (r₂₅). Это может свидетельствовать о наличии мультиколлинеарности факторов и требует дальнейшей проверки данного предположения.

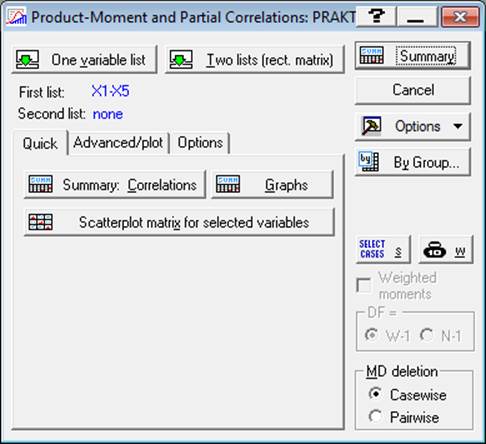
Рис. 3.8. Окно модуля Correlation matrices

После того как получены оценки парных коэффициентов корреляции, необходимо проверить их значимость. Для этого на рис. 3.8. отметим флажком процедуру Corr. Matrix (displayp & N) и щелкнем по клавише OK.

В развернувшемся окне (рис. 3.9) появится корреляционная матрица, дополненная уровнями значимости рассчитанных коэффициентов корреляции. Из приведенных результатов видно, что в данном случае значимыми (р < 0,05) являются только коэффициенты корреляции между переменными

X₁  и  X₃  (r₁₃ = 0,516),   X₁   и  X₄ (r₁₄ = 0,508),   X₂  и  X₅ (r₂₅ = –0,577).

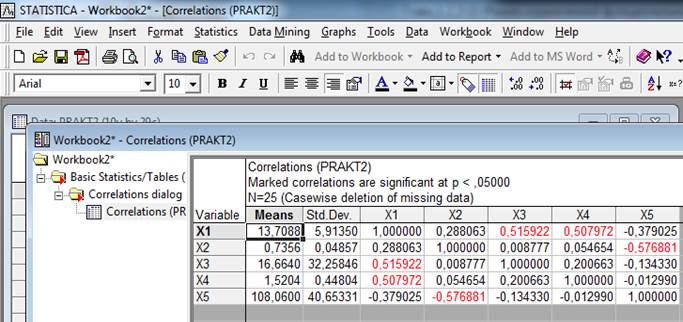
Рис. 3.9. Матрица парных корреляций

Для остальных коэффициентов корреляции полученные значения и уровни их значимости не позволяют отвергнуть гипотезу о равенстве их нулю (рис. 3.10).

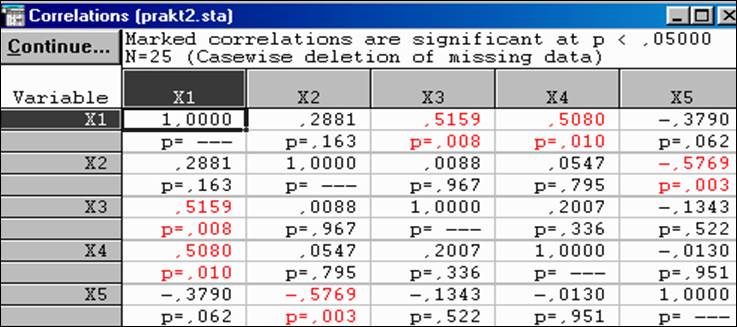
Рис. 3.10. Парные коэффициенты корреляции и уровни их значимости

Одним из простых приемов проверки наличия мультиколлинеарности факторов является сравнение с нулем определителя корреляционной матрицы. Проверяем гипотезу  Н₀: |R| = 1.  В данном примере определитель матрицы R равен

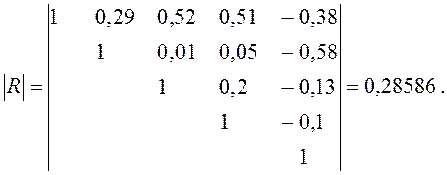
Для проверки гипотезы воспользуемся критерием Уилкса

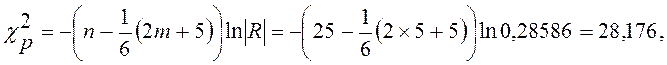
а табличное (критическое) значение для уровня значимости α = 0,01 и числа степеней свободы  ν = 0,5m(m – 1) = 0,5 × 5(5 – 1) = 10 равно χ²_кр = 23,209.  Поскольку χ²_кр < χ²_р нулевая гипотеза отклоняется, т.е. определитель |R| ≠ 1, следовательно, наличие мультиколлинеарности факторных признаков считается доказанным.

2. Для продолжения анализа корреляционной связи между переменными необходимо исключить одну из двух факторных переменных, порождающих мультиколлинеарность (X₂илиX₅). Судя по значениям парных линейных коэффициентов корреляции (r₁₂ = 0,288  r₁₅ = –0,379), из рассмотрения следует удалить переменную X₂, так как у нее слабее связь с зависимой переменной X₁.