Из каждой группы предприятий были сформированы две выборки неравных объемов. Результаты выборочного наблюдения представлены в табл. 1.3.
Таблица 1.3
Первая группа |
Вторая группа |
||||
|
Номер объекта |
X1 |
X2 |
Номер объекта |
X1 |
X2 |
|
1 |
25 |
3,25 |
1 |
32 |
2,90 |
|
2 |
20 |
2,85 |
2 |
30 |
2,94 |
|
3 |
35 |
2,90 |
3 |
41 |
3,00 |
|
4 |
28 |
3,25 |
4 |
34 |
2,75 |
|
5 |
40 |
4,90 |
5 |
20 |
3,30 |
|
6 |
31 |
2,65 |
6 |
46 |
3,43 |
|
7 |
28 |
4,00 |
7 |
35 |
2,80 |
|
8 |
48 |
3,90 |
|||
|
9 |
50 |
5,24 |
|||
В таблице X1 — валовая добавленная стоимость на одного работника, тыс. ден. ед.; X2 — фондоотдача основных производственных фондов, ден. ед.
По приведенным выше данным следует оценить существенность различий двух групп предприятий по Х1 и X2 при a = 0,01.
Решение. Для того чтобы решить поставленную задачу, проверим гипотезу о равенстве векторов средних значений двух выборочных совокупностей.
1. Определим векторы средних значений и совместную ковариационную матрицу S*, необходимые в последующем для расчета Т2-критерия
![]() =
(34 3,66);
=
(34 3,66); ![]() = (34 3,02),
= (34 3,02),
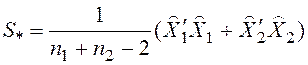 =
=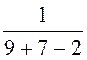
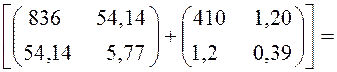
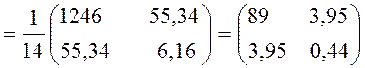 , следовательно, обратная матрица равна
, следовательно, обратная матрица равна 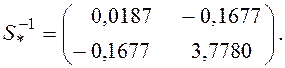
2. Теперь можно рассчитать наблюденное (расчетное) значение общего Т2-критерия Хотеллинга:
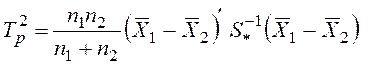 =
=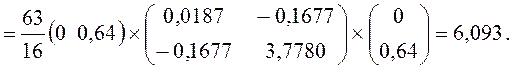
3. Найдем критическое значение Т2-критерия
и произведем сравнение значений ![]() и
и ![]()
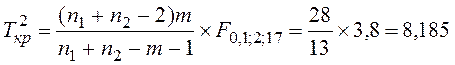 .
.
Поскольку рассчитанное значение ![]() меньше Ткр2 =
8,185, нулевую гипотезу о равенстве векторов средних значений следует принять и
сделать вывод о несущественном влиянии различных условий функционирования
предприятий.
меньше Ткр2 =
8,185, нулевую гипотезу о равенстве векторов средних значений следует принять и
сделать вывод о несущественном влиянии различных условий функционирования
предприятий.
Пример 3. Для того чтобы оценить уровень различия двух групп инженерно-технических работников на предприятиях легкой промышленности (мужчины и женщины) по двум признакам, было проведено выборочное обследование. В выборку попали 20 человек (10 мужчин и 10 женщин). Результаты наблюдения представлены в табл. 1.4.
Таблица 1.4
Мужчины |
Женщины |
||
|
Х1 |
Х2 |
Х1 |
Х2 |
|
4 |
9,0 |
20 |
7,2 |
|
15 |
8,2 |
8 |
6,0 |
|
17 |
10,0 |
12 |
9,2 |
|
20 |
8,0 |
6 |
6,5 |
|
22 |
6,5 |
5 |
7,5 |
|
30 |
8,5 |
18 |
8,0 |
|
20 |
7,5 |
15 |
8,4 |
|
7 |
7,0 |
25 |
9,0 |
|
18 |
9,7 |
10 |
8,1 |
|
4 |
8,4 |
17 |
7,8 |
В таблице Х1 — стаж работы, лет; Х2 — средняя дневная заработная плата, ден. ед.
Проверьте гипотезу о сходстве двух групп работающих: а) по каждому признаку отдельно; б) по двум признакам вместе.
Решение. 1. Для каждой группы отдельно и для совокупности в целом рассчитаем средние значения и дисперсии анализируемых признаков.
I группа (мужчины)
![]()
![]() Ковариационная
матрица S1 равна
Ковариационная
матрица S1 равна
![]()
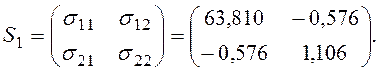
II группа (женщины)
![]()
Ковариационная матрица S2 равна
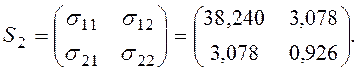
2. Вычислим совместную ковариационную матрицу для двух групп (S*)
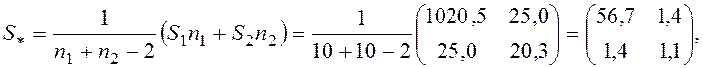
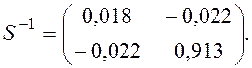
Вычислим расчетное значение Т2-критерия Хотеллинга
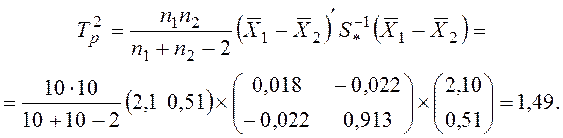
Табличное значение критерия
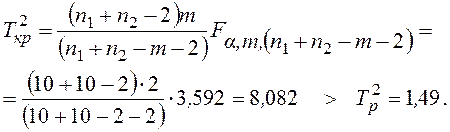
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.