Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 2

В многомерном статистическом анализе проверка гипотезы о равенстве вектора средних значений заданному вектору основывается на тех же подходах, что и для одномерных величин. Но в этом случае мы имеем дело уже с m-числом выборочных средних, т.е. с вектором средних значений: . Вектор  сравнивается с постоянным вектором  m = (m₁, m₂,  ..., m_m). Прямая гипотеза имеет вид

H₀: ,  при альтернативной   H₁:.

Для проверки многомерной гипотезы данного вида используется критерий, известный как критерий Хотеллинга

                                       (1.1)

где 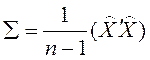— ковариационная матрица; Х— матрица с центрированными значениями переменной: .

Расчетное значение () сравнивается с критическим значением, исчисляемым при заданном уровне вероятности () и числе степеней свободы     и  

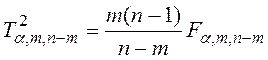.                                     (1.2)

В формуле (1.2) F_a,m,n–m — табличное значение F-критерия Фишера для числа степеней свободы   и  . Многомерная гипотеза о равенстве вектора средних величин заданному вектору подтверждается при .

Пример 1. Для предприятий розничной торговли в административном районе установлены следующие нормативные показатели эффективности деятельности: средний уровень рентабельности хозяйственной деятельности — 20 %  и средняя продолжительность оборота оборотных средств — 12 дней. Предположим, что более низкие значения уровня рентабельности и скорости оборота означают нарушение ритмичности товарно-денежных операций  и снижение конкурентоспособности предприятий торговли.

С целью оперативного контроля за результатами коммерческой деятельности торговых предприятий района проведен анализ эффективности торговой деятельности и получены следующие данные (табл. 1.2).

Таблица 1.2

Рентабельность торговой деятельности и оборачиваемость оборотных средств предприятий

Номер объекта	Рентабельность, %	Продолжительность оборота, дней
01 02 03 04 05 06 07 08 09 10 11 12	14 12 16 14 15 18 22 20 13 19 12 14	19 15 19 17 24 12 10 15 18 20 22 23
Среднее значение	15,8	17,8

Оценим существенность различий между фактическими значениями рассматриваемых показателей и установленными нормативами. Уровень значимости    зададим равным  0,05.

Решение. Определим следующие параметры многомерной случайной величины:

вектор средних значений ` = (15,8 17,8);

ковариационная матрица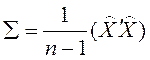

××

×  = × = .

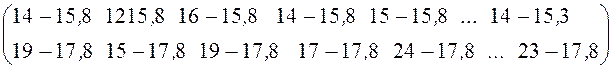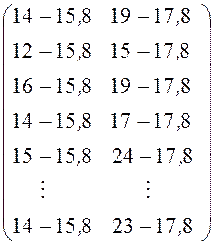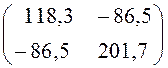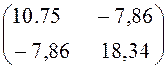Обратная ковариационная матрица  Σ^–1 будет равна

.

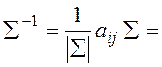
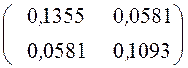Рассчитаем фактическое значение Т²-критерия Хотеллинга

´

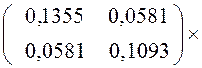
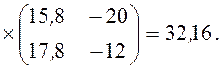
Критическое значение для заданного уровня значимости   = 0,05 составит

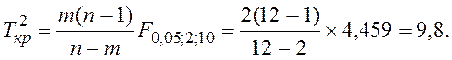
Как видим, расчетное значение -критерия почти в три раза превосходит критическое (32,16 > 9,8), что свидетельствует о существенности расхождения между фактическими и нормативными значениями анализируемых показателей.

1.1.2. Проверка гипотезы о равенстве двух векторов средних значений

В многомерном статистическом анализе проверяется гипотеза о равенстве  векторов средних значений многомерных величин

,

, или в векторной форме

;   и   .

Для проверки данной гипотезы применяется многомерный Т²-критерий, исчисляемый по формуле

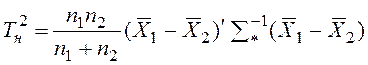,                            (1.3)

где  `Х<sub>1</sub>, `Х₂ — векторы средних значений;  — обратная матрица, рассчитанная для объединенной ковариационной матрицы

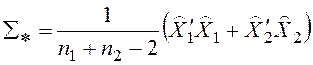, где  — матрица центрированных значений .

Критические значения для  Т² находятся по формуле

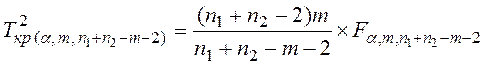.                   (1.4)

При  нулевая гипотеза  принимается с вероятностью (1–). Если же  , то нулевая гипотеза о равенстве векторов средних значений отвергается.

Пример 2. С целью анализа различий показателей производственно-хозяйственной деятельности родственных предприятий, расположенных в рамках свободной экономической зоны (первая группа) и за ее пределами (вторая группа), было проведено выборочное обследование.