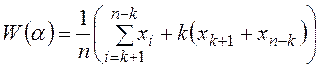Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 8

.                               (2.6)

По аналогии с оценками    и   по усеченной совокупности могут быть найдены не только средние величины, но и другие характеристики статистической совокупности, например, меры вариации, мода, медиана.

Широкое распространение при определении устойчивых оценок получил также подход Хубера, при котором используется некоторая исходная величина k,  определяемая с учетом степени «засорения» статистической совокупности  (x) (см. параграф 2.4). Расчеты в этом случае повторяются (имеют итеративный характер) и в итоге приводят к наилучшим оценкам.

Оценка средней величины по методу Хубера  производится  по формуле

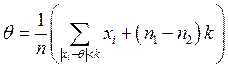,                              (2.7)

где  q — устойчивая оценка среднего значения; k — допустимая величина отклонения oт центра совокупности (определяется с учетом удельного веса грубых ошибок в совокупности данных  (x)); n₁ — численность группы наблюдений из совокупности, отличающихся наименьшими значениями  x_i  < q– k,  или значения в интервале (–¥; q– k); n₂ — численность группы наблюдений из совокупности, отличающихся наибольшими значениями x_i  < q + k,  или значения в интервале (q + k; ¥).

При расчетах по формуле (2.7) в качестве начальной оценки (q) может быть использована средняя арифметическая или медиана, рассчитанные по выборке. На каждой итерации производится разделение выборочной совокупности на три класса. В первый класс попадают значения признака, которые остаются без изменения . Во второй и третий классы (для  x_i > q + k  и  x< q– k) — «грубые ошибки». Причем они не исключаются из рассмотрения, а модифицируются — заменяются соответственно на величины  (x –– k)  и  (x_i +k). По исходным  и модифицированным значениям при каждой итерации определяется новая оценка средней (q). Процесс продолжается до тех пор, пока все наблюдения не оказываются в интервале «истинных» значений .

В многомерном случае «засорением» совокупности данных уже будут не отдельные значения, а вектор значений, характеризующий аномальное наблюдение.

Чтобы проверить, является ли многомерное наблюдение аномальным, обычно используют расстояние Махаланобиса

,                                     (2.8)

где  — вектор значений признака у «подозреваемого» объекта;  — вектор средних значений для многомерной совокупности данных; å — матрица ковариаций.

В этом случае критерий  (F)  для проверки гипотезы о существенности отклонения случайного вектора  X  строится следующим образом:

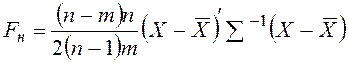.                          (2.9)

Если при заданном уровне значимости  и числе степеней свободы n₁ = m  и n₂ = n – m- 1 окажется, что  , то проверяемое наблюдение  действительно признается аномальным. В противном случае, когда  , отклонение проверяемого вектора от вектора средних значений считается приемлемым, а гипотеза о «засорении» совокупности отвергается.

К выявленным грубым ошибкам в многомерной совокупности можно применять уже известные для одномерного случая приемы обработки данных.

2.2. Примеры решения типовых задач

Пример 1. На основании приведенных ниже данных по предприятиям пищевой промышленности проверьте гипотезу о наличии грубых ошибок (аномальных наблюдений) в начале и в конце ранжированного ряда по каждой переменной (табл. 2.1).

Таблица 2.1