Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 23

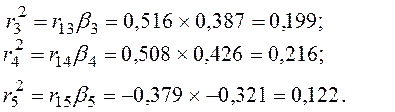
Множественный коэффициент детерминации равен R² = 0,538, а множественный коэффициент корреляции R= 0,734. Проверим правильность расчетов. Множественный коэффициент детерминации равен сумме частных коэффициентов

Итак, на долю переменной  Х₃  приходится около 20 % объясненной дисперсии зависимой переменной Х₁, на долю  Х₄ — 21,6 %, на долю  Х₅ — 12,2 %. Следовательно, в данном варианте переменная  Х₅  является наименее значимой по своему влиянию на зависимую переменную Х₁.

Что касается множественных коэффициентов детерминации и корреляции, то их значения уменьшились, но незначительно.

3.4. Контрольные задания

Задание 1. На основании данных, приведенных в табл. 3.7, проведите анализ зависимости индекса уровня человеческого развития от объемов государственного финансирования систем образования и здравоохранения.

Таблица 3.7

Страна	Х1	Х2	Х3
Германия	0,925	4,8	7,9
Бельгия	0,939	3,1	6,3
Дания	0,936	8,1	6,9
Франция	0,928	6,0	7,3
Греция	0,885	3,1	4,7
Великобритания	0,928	5,3	5,8
Ирландия	0,925	6,0	5,2
Италия	0,913	4,9	5,8
Люксембург	0,925	4,0	5,7
Нидерланды	0,935	5,1	6,0
Португалия	0,880	5,8	5,1
Испания	0,913	5,0	5,4
США	0,939	5,4	5,7

Здесь: Х₁ — индекс человеческого развития за 2000 г.; Х₂ — государственные расходы на образование в процентах к ВВП за 1995—1997 гг.; Х₃ — государственные расходы на здравоохранение в процентах к ВВП за 1998 г.

Постройте линейную регрессионную модель зависимости переменной Х₁ от переменных Х₂  и Х₃ . В матричном виде рассчитайте парные и множественные коэффициенты корреляции и детерминации и оцените их значимость. Поясните полученные результаты и сделайте выводы.

Задание 2. По приведенным данным табл. 3.8 о результатах производственной и коммерческой деятельности в 14 хозяйствах области рассчитайте матрицу парных коэффициентов корреляции, проверьте ее на наличие мультиколлинеарности независимых переменных. Постройте модели линейной регрессии относительно зависимой переменной (Х₁) в натуральном и стандартизованном масштабах.

Таблица 3.8

Номер хозяйства	Х1	Х2	Х3	Х4
1	460	1735	1141	649
2	937	3959	2110	448
3	1603	7441	2709	2549
4	1003	3650	1650	835
5	1037	5140	2753	589
6	677	3587	2164	330
7	558	3239	1507	684
8	2793	10610	4699	2327
9	1925	11604	3865	2498
10	1036	4714	1795	795
11	772	4345	2245	632
12	1156	5777	2739	1155
13	1391	5834	2908	1383
14	677	3290	1721	723