Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 17

Рассмотрим экономический смысл полученных коэффициентов регрессии для нашего примера. Первый коэффициент a₁ = -1,6 показывает, что при увеличении нагрузки пашни на одного работника на 1 га объем выпуска продукции сельского хозяйства уменьшится на 1,6 млн ден. ед. Второй коэффициент регрессии  a₂ = 6,8 показывает, что при увеличении производительности труда одного работника на 1 тыс. ден. ед., объем выпуска продукции увеличится на 6,8 млн ден. ед. при прочих равных условиях.

1.  Для расчетов коэффициентов корреляции и детерминации (парных и множественных) проведем прежде всего стандартизацию исходных переменных и рассчитаем матрицу корреляций  R

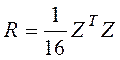, где  Z — матрица стандартизованных значений переменных

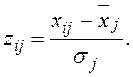
Матрица  Z^ТZбудет иметь следующий вид:

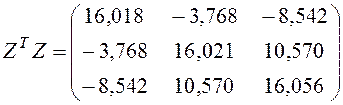, а матрица корреляций будет равна

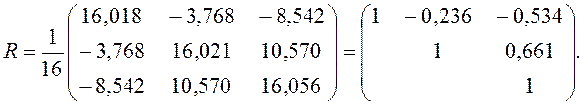
Теперь рассчитаем множественный коэффициент детерминации (R²) и множественный коэффициент корреляции  R_{y, x1, x2}

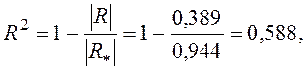
Полученные результаты позволяют сделать следующий вывод: вариация объема выпуска продукции на 58,8 % зависит от исследуемых признаков-факторов; связь между результативным признаком (откликом) достаточно тесная, поскольку множественный коэффициент корреляции близок к единице 

Пример 4.На основе приведенных данных табл. 3.3 по десяти промышленным предприятиям проведите регрессионный анализ зависимости себестоимости произведенной продукции Y (млн ден. ед.) от объема произведенной продукции  (млн ден. ед.) и уровня производительности труда рабочих  (тыс. ден. ед. на чел.).

Таблица 3.3

Решение. 1. Определим вектор оценок коэффициентов регрессии  А  уравнения

.

Согласно методу наименьших квадратов, вектор A получается из выражения , где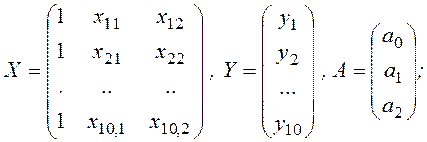                            

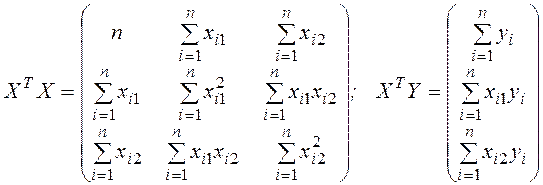
Для того чтобы рассчитать все необходимые элементы матрицы Х^ТХ и вектора Х^ТYзаполним табл. 3.4.

Таблица 3.4