Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 22

Рассчитаем два уравнения регрессии: первое, включающее все факторные переменные, а второе — без значений переменной  X₂.

I вариант. Расчет уравнения регрессии по значениям всех факторных переменных и зависимой переменной X₁.

В окне переключения модулей  выбираем модуль MultipleRegression.

Рис. 3.11. Окно переключения модулей

В раскрывшемся окне указываем зависимую переменную X₁ и независимые переменные X₂, X₃, X₄, X₅.  Щелкаем по кнопке OK,и на экране разворачивается окно с основными процедурами регрессионного анализа (рис. 3.12).

Рис. 3.12. Предварительные результаты множественной регрессии

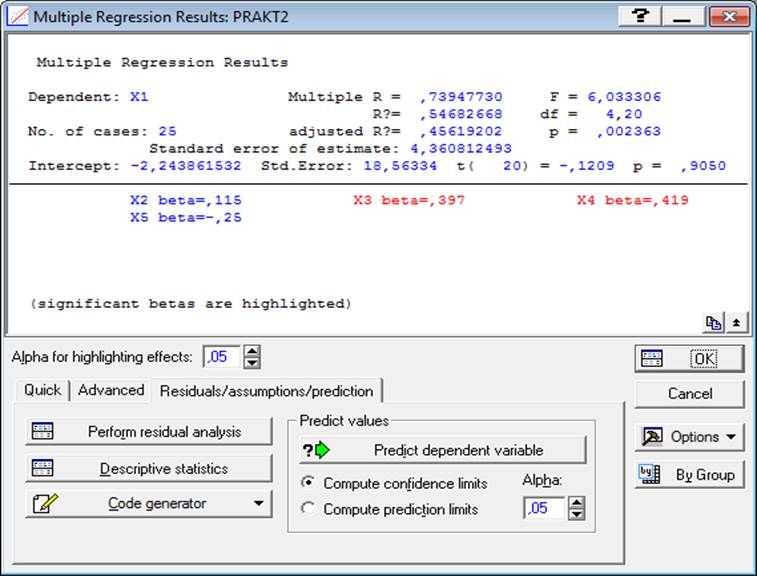
Dep. Var — зависимая переменная X₁; Multiple R — множественный коэффициент корреляции R = 0,739; Standarderrorofestimate — стандартная ошибка аппроксимации A = 4,36 %; Intercept — свободный член уравнения a₀ = -2,244; Std. Error — стандартная ошибка свободного члена = 18,56 %.

Анализ полученных результатов показывает, что связь между зависимой переменной X₁ (уровень рентабельности производства) и факторными переменными (Х₂, Х₃, Х₄, Х₅) достаточно тесная (R = 0,739). Судя по величине множественного коэффициента детерминации (R² = 0,547),  вариация X₁ на 54,7 % определяется рассматриваемыми факторами.

Чтобы получить на экране само уравнение регрессии, в активном окне (рис. 3.12)  щелкнем по кнопке RegressionSummary.

Результаты расчетов приведены на рис. 3.13. Поясним их смысл.

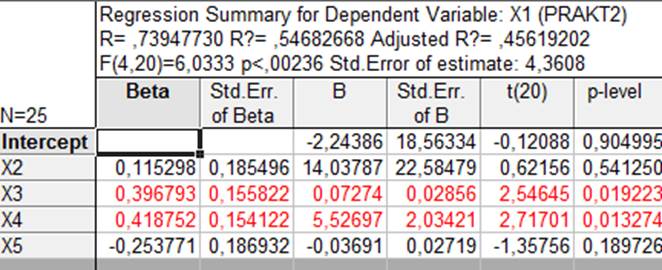
Рис. 3.13. Уравнение регрессии и его оценки для первого варианта

Уравнение регрессии будет иметь вид

Для проверки значимости полученного уравнения регрессии в целом воспользуемся  F-критерием Фишера. Расчетное значение F_р = 6,033, а табличное значение при числе степеней свободы в числителе 4, а в знаменателе 20, равно F_кр = 2,87. Так как F_р > F_кр., уравнение регрессии в целом следует считать значимым.

На рис. 3.12 под чертой указаны значения b-коэффициентов для каждой переменной:  b₂ = 0,115;  b₃ = 0,397;  b₄ = 0,419;  b₅= -0,25.

Для того чтобы определить влияние отдельных факторов на зависимую переменную, исчислим частные коэффициенты детерминации (r²_j)

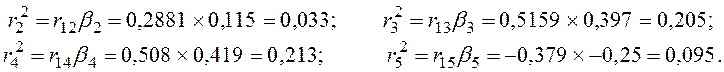
Проверим правильность расчетов

Итак, на долю переменной  Х₂ приходится 3,3 % объясненной дисперсии зависимой переменной, на долю  Х₃ — 20,5 %, на долю  Х₄ — 21,3 % и на долю  Х₅ — 9,5 %. Следовательно, переменная  Х₂  является наименее значимой по своему влиянию на зависимую переменную  Х₁.

II вариант. Расчет уравнения регрессии после удаления значений переменной X₂, порождающей мультиколлинеарность (рис. 3.14).

Аналогично тому, как это было сделано в первом варианте, выполним все расчеты без переменной Х₂.

Уравнение регрессии будет иметь вид

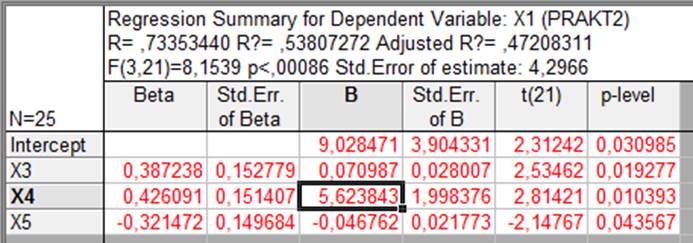
Рис. 3.14. Уравнение регрессии и его оценки для второго варианта

Если сравнить его с уравнением, рассчитанным для первого варианта анализа, то мы увидим, что незначительно изменились коэффициенты регрессии для оставшихся переменных, но одновременно довольно сильно изменилось значение свободного члена уравнения.

Оценка нового уравнения по F-критерию Фишера показывает расчетное значение F-критерия — F_р = 8,154, а табличное значение при числе степеней свободы ν₁ = 3  ν₂ = 21 и уровне значимости α = 0,05 равно F_кр = 3,072. Так как F_р > F_кр, то уравнение регрессии в целом следует считать значимым.

Повторим также анализ множественных коэффициентов корреляции и детерминации. Для этого нам понадобится новая матрица корреляций (рис. 3.15).

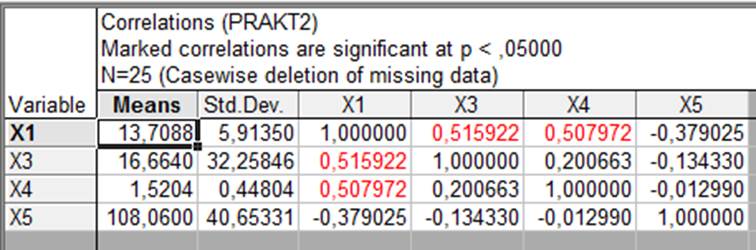
Рис. 3.15. Парные коэффициенты корреляции для второго варианта анализа

Новые значения b-коэффициентов для переменных равны:  b₃ = 0,387;  b₄ = 0,426;  b₅ = -0,321. Для того чтобы определить влияние отдельных факторов на зависимую переменную, исчислим частные коэффициенты детерминации (r²_j):