Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 7

При робастном оценивании решаются задачи двух основных типов:

- при помощи специальных критериев в статистической совокупности выявляются аномальные наблюдения;

- при помощи одного из выбранных методов исчисляются устойчивые (робастные) оценки совокупности данных, в частности при нормальном законе распределения определяют среднее значение и дисперсию.

В некоторых случаях аномальное наблюдение в статистической совокупности можно обнаружить при помощи визуального анализа. Но чаще приходится использовать специальные статистические приемы и методы. Рассмотрим некоторые из них.

Выявление грубых ошибок на основании Т-критерия Граббса

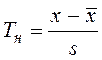,                                                   (2.1)

где  — выборочная средняя;s — выборочное среднеквадратическое отклонение случайной величины.

Расчетные значения  Т-критерия сравнивают с пороговыми значениями, заданными соответствующим распределением. Проверяемые значения переменной относят к классу выбросов, если    ().  Если , то считается, что эти значения несущественно отличаются от других значений  и не являются аномальными для данной совокупности.

Выявление грубых ошибок на основании  L и  Е-критериев Титьена—Мура:

1. L-критерий используется для выявления грубых ошибок среди наименьших значений переменной

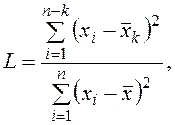                                                (2.2)

где  — значение анализируемого признака у  i-го наблюдения; n — объем выборки; k — число предполагаемых аномальных наблюдений;  — среднее значение признака, рассчитанное по выборке;  — среднее значение признака, рассчитанное по «усеченной» совокупности данных, то есть по  (n – k)  наблюдениям, остающимися после удаления из выборочной совокупности  k грубых ошибок «сверху», т.е. значений, сильно отличающихся от средней в меньшую сторону

.

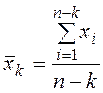2. L'-критерий используется для выявления грубых ошибок среди наибольших значений переменной

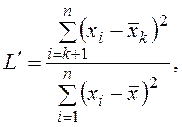                                            (2.3)

где  — среднее значение признака, рассчитанное по «усеченной» совокупности, то есть по  (n – k)  наблюдениям, остающимся после удаления из выборочной совокупности  k  грубых ошибок «снизу»

.

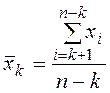3. Е-критерий используется, когда в выборке грубые ошибки расположены симметрично в верхней и нижней части ранжированного ряда значений переменной

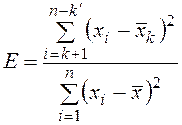,                                              (2.4)

где   — cредняя, рассчитанная по «усеченной совокупности», после удаления наименьших k и наибольших k' подозреваемых значений

.

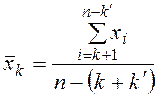Для всех названных критериев  L, L'  и  Е предельные значения при заданном уровне значимости  , известном объеме выборки n и предполагаемом числе ошибок k представлены в специальных таблицах (см. параграф 2.4).  Если рассчитанные значения критериев оказываются меньше табличных  (), то проверяемые значения переменной следует отнести к грубым ошибкам.

2.1.2. Методы устойчивого оценивания параметров статистической

совокупности

После того как при помощи одного из рассмотренных критериев удалось выявить аномальные наблюдения, предстоит исчислить устойчивые (робастные) оценки среднего значения и дисперсии.При этом, как уже говорилось, используются два основных подхода: аномальные значения (грубые ошибки) либо удаляются из совокупности, либо модифицируются.

Наиболее простым способом устойчивую оценку средней можно получить по усеченной совокупности данных. Для этого из совокупности предварительно удаляются наблюдения, являющиеся грубыми ошибками. Американский статистик Пуанкаре предложил следующую формулу для расчета средней по усеченной совокупности

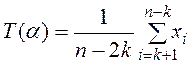.                                            (2.5)

В данной формуле  k — это число грубых ошибок,   — есть целая часть от произведения  ,  где  n — объем выборочной совокупности, а   — некоторая функция величины засорения выборки (x), значения которой находят по специальным таблицам (см. параграф 2.4.).

Другой подход к исчислению устойчивой средней, предложенный Винзором, предполагает замену аномальных значений переменной модифицированными значениями. Средняя по Винзору определяется с известным заранее уровнем   (0 <  < 0,5),  по формуле