Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 15

По таблице значений t-критерия Стьюдента для заданного уровня значимости и числа степеней свободы (n – m – 1) находят t_кр. Значимость проверяемого коэффициента a_jподтверждается, если   |t_р| > t_кр. В противном случае коэффициент регрессии незначим, и соответствующая ему переменная не должна входить в модель.

Аналогичным образом осуществляется проверка значимости парных и частных коэффициентов корреляции. При этом табличное значение определяется для числа степеней свободы, равного (n – m – 1), а расчетное значение критерия вычисляется по формуле

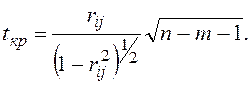                                   (3.10)

Значимость множественного коэффициента детерминации (R²_0/1,2…m) и соответственно множественного коэффициента корреляции (R_0/1,2…m) оценивается по F-критерию Фишера. Расчетное значение этого критерия определяется по формуле

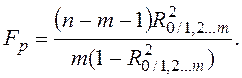                                     (3.11)

Гипотеза о значимости множественного коэффициента детерминации принимается в том случае, если  F_р > F_кр  для заданного уровня значимости  α  и числа степеней свободы ν₁ = m  и  ν₂ = n – m – 1. 

3.2. Примеры решения типовых задач

Пример 1.По результатам корреляционно-регрессионного анализа вычислены матрица парных коэффициентов корреляции и значения β-коэффициентов

;     .

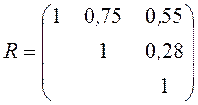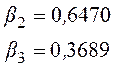Известно, что откликом (Y) является первая переменная (X₁), а число наблюдений (n) равно 20.

1. Рассчитаем частные и множественный коэффициенты детерминации и корреляции. Проанализируем полученные результаты и сделаем вывод.

2. Произведем оценку значимости коэффициентов. В анализе корреляции будем использовать  t-критерий Стьюдента.

Решение. 1. Для оценки тесноты корреляционной связи рассчитаем следующие величины:

- определители матрицы парных корреляций (R) и матрицы  R_*

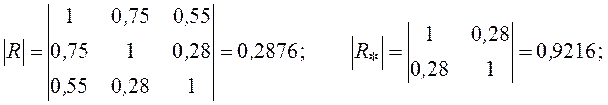
- множественный коэффициент детерминации ()

;

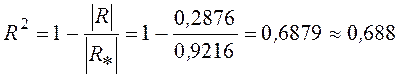- множественный коэффициент корреляции (R)

.

Следовательно, связь между факторными признаками и откликом тесная, поскольку значение множественного коэффициента близко к единице; вариация результативного показателя на 68,8 % определяется признаками-факторами;

- частные коэффициенты детерминации равны соответственно

 или 48,5 %;

 или 20,3 %.

На долю первого фактора приходится 48,5 % объясненной дисперсии результативного показателя, а на долю второго фактора — 20,3 %.

Выполним проверку правильности расчетов

 (68,8 %).

Таким образом, два фактора объясняют примерно 68,8 % вариации результативного показателя.

2. Оценим значимость парных коэффициентов корреляции по t-критерию Стьюдента.

Расчетное значение критерия определяем по формуле

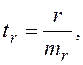
где  — ошибка коэффициента корреляции. Ее находят по формуле

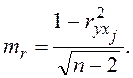
Определяем  для   и  для  :

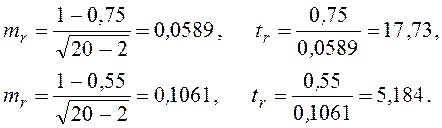
Критическое значение t-критерия для уровня значимости α = 0,05 равно 1,725. Поскольку в обоих случаях t_r > t_кр, проверяемая гипотеза отвергается, т.е. парные коэффициенты корреляции являются значимыми.

Пример 2. По пяти промышленным предприятиям имеются следующие данные о фондовооруженности труда рабочих (Х₁), уровне производительности труда (Х₂), удельном весе потерь от брака (Х₃) (табл. 3.1).

Таблица 3.1

Номер предприятия	Фондовооруженность труда рабочего, тыс. ден. ед.	Месячная производительность труда рабочего,  тыс. ден. ед.	Удельный вес потерь от брака, %
	Х1	Х2	Х3
1	3,9	7,0	2,4
2	1,1	11,1	5,9
3	1,8	10,2	6,2
4	6,0	12,0	6,0
5	5,4	10,0	11,0

Определите:

1)  матрицы парных и частных коэффициентов корреляции;