Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 16

2)  множественный коэффициент детерминации и множественный коэффициент корреляции при условии, что  — зависимая переменная;

3)  матрицу ковариаций.

Решение. 1. Парные коэффициенты корреляции рассчитываются следующим образом:

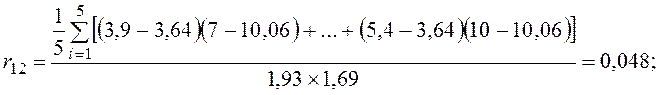
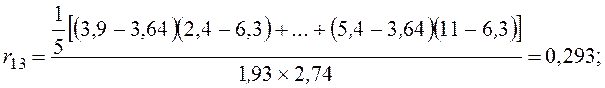
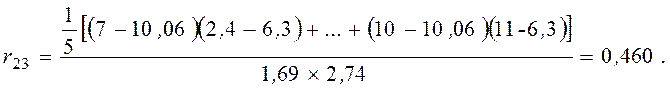
Матрица парных коэффициентов корреляции имеет вид

.

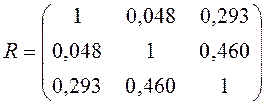2. Частные коэффициенты корреляции рассчитываются по формуле

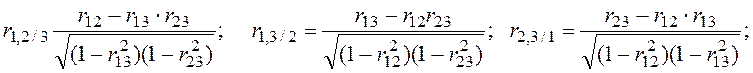
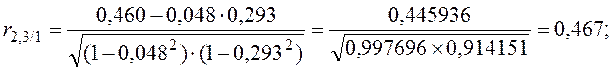
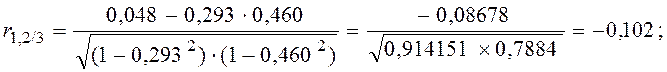
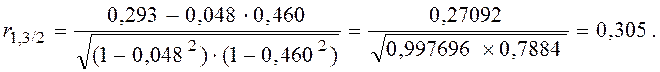
Матрица частных коэффициентов корреляции (R′) будет иметь вид

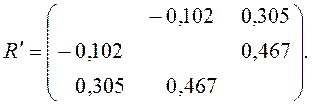
3. Множественный коэффициент корреляции определяется по формуле

           

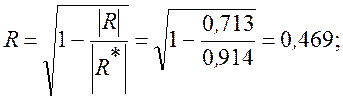
4. Элементы ковариационной матрицы cov(x_i, x_j) определяются по формуле

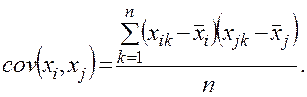
В многомерном статистическом анализе ковариации принято иногда обозначать как σ_ij (по аналогии с дисперсиями).

Рассчитаем последовательно все элементы ковариационной матрицы

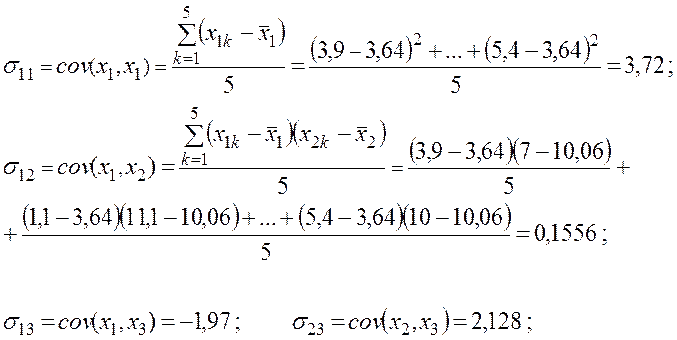
Матрица ковариаций будет иметь следующий вид:

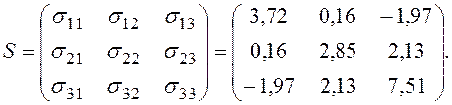
На основании матрицы ковариаций можно сравнить вариацию признаков в исследуемой статистической совокупности. Для этого рассчитаем коэффициенты вариации по каждой переменной

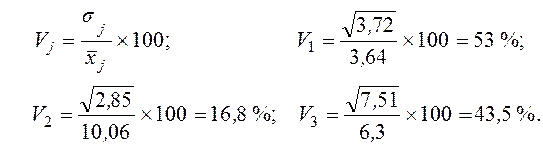
Как показывают расчеты, исследуемая совокупность наиболее однородна по второй переменной  X₂ — месячная производительность труда, а наименее однородна по переменной  X₁ — фондовооруженность труда рабочего.

Используя элементы ковариационной матрицы, можно также проверить правильность расчета парных линейных коэффициентов корреляции

Например, коэффициент корреляции между переменными x₁ и x₂  будет равен

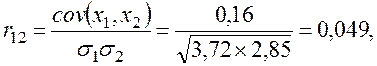
а в корреляционной матрице он равен 0,048, т.е. имеется небольшое расхождение за счет округлений.

Пример 3. На основании приведенных данных табл. 3.2 по районам области постройте линейную регрессионную модель валового выпуска продукции сельского хозяйства в целом по области.

Таблица 3.2

Окончание табл. 3.2

Здесь: Х₁ —  нагрузка пашни на одного работника, га; Х₂ — производительность труда одного работника, тыс. ден. ед.; Y— валовая продукция, млн ден. ед.

1. Рассчитайте уравнение множественной линейной регрессии.

2. Оцените тесноту связи между анализируемыми признаками с помощью коэффициентов корреляции и детерминации (парных и множественных).

3. Оцените значимость коэффициентов регрессии по t-критерию Стьюдента и качество модели по F-критерию Фишера. Поясните экономический смысл полученных результатов.

Решение. 1. Для оценки коэффициентов уравнения регрессии воспользуемся методом наименьших квадратов (МНК).

С этой целью строим систему нормальных уравнений для матрицы исходных значений переменных:

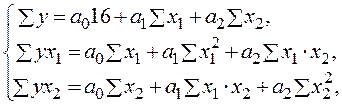
390;                            10142;

   3232,5;

    

Система уравнений будет иметь вид

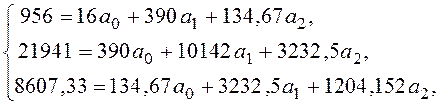
Уравнение регрессии можно записать следующим образом: