Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 10

Модифицированные значения переменных рассчитываются следующим образом:  во втором классе от каждого значения отнимаем  k = 1,399, а в третьем классе к каждому значению переменной прибавляем  k.

Новое значение оценки величины θ определяется по модифицированным данным следующим образом:

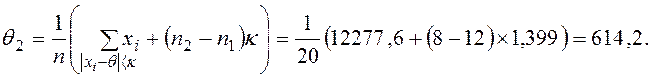
Следующую итерацию начнем уже с данных, модифицированных на первом шаге (табл. 2.4). Тогда границы классов будут иметь следующий вид:

І класс:  |x_i – θ| < k      θ – k < x_i < θ + k614,2 - 1,399 < x_i < 614,2 + 1,399,

ІІ класс:  θ + k < x_i614,2 + 1,399 < x_i615,6 < x_i,

ІІІ класс:  x_i < θ – kx_i < 614,2 – 1,399x_i < 612,8.

Таблица 2.4

Как видно из расчетов, после второй итерации ни одно значение не перешло в І класс. Пересчитаем новую оценку средней  θ

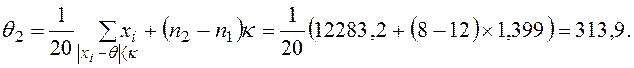
Границы классов будут иметь следующий вид:

І класс:  |x_i – θ| < k,      θ – k < x_i < θ + k,  613,9 – 1,399 < x_i < 613,9 + 1,399;

ІІ класс:   θ + k < x_i,613,9 + 1,399 < x_i,615,3 < x_i;

ІІІ класс:  x_i < θ – k,  x_i < 613,9 – 1,399,x_i < 612,5.

Поскольку значение оценки средней после очередной модификации изменились незначительно, можно предположить, что для достижения конечной цели (все значения попадают в І класс) потребуется очень большое число итераций.

2.3. Контрольные задания

Задание 1. В ходе текущего контроля содержания загрязняющих веществ в воздухе были получены следующие данные (табл. 2.5).

Таблица 2.5

Используя критерии Граббса и Титьена—Мура, проверьте наличие грубых ошибок (аномальных наблюдений) и рассчитайте устойчивые оценки средней по Пуанкаре и Винзору.

Задание 2.В результате ежедневного наблюдения за качеством производимой продукции в разные смены были получены следующие данные (табл. 2.6).

Таблица 2.6