Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 20

Рисунок 3.8 Выбор процедур анализа остатков

Observedvalue— наблюдаемые значения (Y); Predictedvalue— расчетные значения (Y_х); Residual — остатки (Y—Y_х); Standardpred. v— стандартизованные значения переменной; Standardresidual— стандартизованные значения остатков; Std. Err. Pred. val— стандартные ошибки расчетных значений и другие характеристики.

В последних строках таблицы приведены обобщающие характеристики переменных (минимальное, максимальное, среднее значения и медиана). На рис. 3.9 представлен график расчетных значений переменной и остатков.

Рис. 3.9 Результаты расчетов на основании уравнения регрессии

По характеру распределения остатков можно судить о том, являются ли они случайными величинами или зависят от величины результативной переменной. В данном примере характер рассеяния остатков свидетельствует о том, что они являются случайными величинами. Следовательно, применение метода наименьших квадратов для нахождения оценок коэффициентов регрессии оправдано.

Модуль «Анализ остатков» (Residual analysis) позволяет также визуально оценить близость фактических и рассчитанных значений переменной. Для этого в меню модуля (см. рис. 3.4) нужно выбрать функцию Pred. & residuals (кнопка D).

В развернувшемся окне будет представлен следующий график остатков (рис. 3.10).

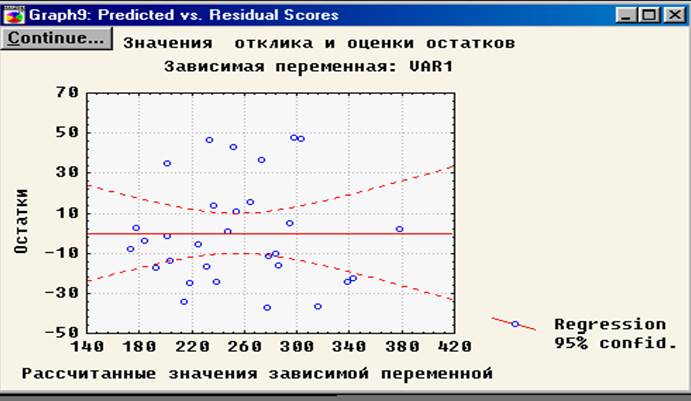
Рис. 3.10. График рассеяния остатков зависимой переменной

Судя по расположению точек на графике, можно утверждать, что построенная регрессионная модель хорошо аппроксимирует фактические значения зависимой переменной.

Задание 2.

По приведенным ниже данным о работе 25 предприятий проведите корреляционный анализ взаимосвязи изучаемых признаков. Проверьте матрицу парных корреляций (R) на наличие мультиколлинеарности факторов.

Постройте две линейные регрессионные модели относительно отклика Х₁, одну — по значениям всех факторных признаков, и вторую — без значений признака, порождающего мультиколлинеарность. Укажите «наилучшую» регрессионную модель и сделайте выводы (табл. 3.6).

Таблица 3.6

Номер объекта	Х1	Х2	Х3	Х4	Х5
1	13,26	0,78	12,3	1,45	166,3
2	10,16	0,75	10,4	1,30	92,8
3	13,72	0,68	18,0	1,37	158,0
4	12,85	0,70	4,3	1,65	93,9
5	10,63	0,62	8,8	1,91	173,9
6	9,12	0,76	5,7	1,68	162,3
7	25,83	0,73	170	1,94	88,6
8	23,39	0,71	17,8	1,89	101,2
9	14,68	0,69	8,8	1,94	166,3
10	10,05	0,73	6,0	2,06	140,8
11	13,99	0,68	8,2	1,96	128,5
12	9,68	0,74	8,4	1,02	177,8
13	10,03	0,66	6,7	1,35	114,5
14	9,13	0,72	10,4	0,88	93,2
15	5,37	0,68	6,6	0,62	126,7
16	9,86	0,77	8,6	1,09	91,8
17	12,62	0,78	7,9	1,60	69,1
18	5,02	0,78	3,4	1,53	66,1
19	21,18	0,81	16,0	1,40	67,7
20	25,17	0,79	14,6	2,22	50,4
21	19,40	0,77	12,7	1,32	70,6