Проверка многомерных статистических гипотез. Проверка гипотезы о равенстве вектора средних значений заданному вектору, страница 13

Таблица 2.12

Значения  k = f()  для расчета устойчивой оценки  Хубера

ξ	k	ξ	k
0 0,001 0,002 0,005 0,01 0,02 0,05 0,10 0,15	0 2,630 2,435 2,160 1,945 1,717 1,399 1,140 0,980	0,20 0,25 0,3 0,4 0,5 0,65 0,80 1	0,862 0,766 0,685 0,550 0,436 0,291 0,162 0

3. МНОЖЕСТВЕННЫЙ КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ

3.1. Методические рекомендации

Регрессионный анализ — это статистический метод исследования зависимости случайной величины Y-отклик от переменной (X) или переменных  — предикторы;  рассматриваются в регрессионном анализе как неслучайные величины, независимо от истинного закона их распределения. В ходе регрессионного анализа при помощи выбранного метода [7, 16] строится математическая модель, описывающая форму связи переменных — уравнение регрессии. Как правило, регрессионному анализу предшествует анализ корреляционной зависимости переменных, который позволяет установить наличие связи между анализируемыми переменными, оценить ее тесноту и определить направление (прямая или обратная связь). Кроме того, в ходе корреляционного анализа происходит отбор существенных факторов, включаемых в уравнение регрессии. Наиболее простой формой корреляционного анализа является парная корреляция — анализируется связь между парой признаков — откликом  Y  и одним предиктором . В этом случае уравнение регрессии принимает вид y = f(x).

В ходе множественного корреляционного анализа рассчитываются следующие характеристики:

-парные коэффициенты корреляции r_ij — оценки тесноты линейной корреляционной связи между всеми парами анализируемых признаков с учетом их взаимного влияния и взаимодействия. Совокупность парных коэффициентов корреляции, относящихся ко всем исследуемым признакам, может быть представлена в виде корреляционной матрицы  R, которая рассчитывается по формуле

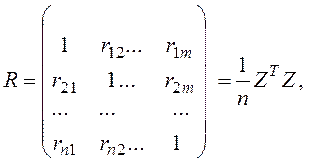                                   (3.1)

где Z — матрица стандартизованных значений исходных переменных. Ее элементы рассчитываются по формуле

На главной диагонали матрицы  R  стоят единицы, т.е. дисперсии стандартизованных переменных, а все другие элементы — парные коэффициенты корреляции  r_ij;

-частные коэффициенты корреляции , характеризующие тесноту линейной корреляционной связи между парой анализируемых признаков (x_i  и  x_j) в условиях элиминирования влияния на эту пару других переменных (x_k, x_m  и т.д.). Эти коэффициенты характеризуют так называемую чистую корреляцию. В матричном виде формулу для расчета частных коэффициентов корреляции можно записать следующим образом:

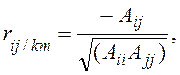                                            (3.2)

где А_ii , A_jj , A_ij  — алгебраические дополнения соответствующих элементов матрицы парных корреляций R.

Знак частному коэффициенту корреляции присваивается такой же, как и у парного коэффициента корреляции;

-множественный коэффициент корреляции R_0/1,2, …_m характеризует степень тесноты связи между результативным признаком (откликом) Y и всеми факторными признаками (предикторами — X_j );

-множественный коэффициент детерминации R²_0/1,2, …_m характеризует долю дисперсии результативной переменной, обусловленную влиянием факторных переменных, участвующих в анализе. На основе корреляционной матрицы  R  множественный коэффициент корреляции и множественный коэффициент детерминации могут быть исчислены следующим образом:

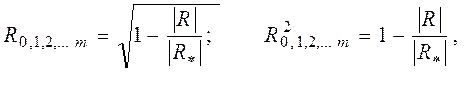                     (3.3)

где  |R|  —  определитель матрицы парных корреляций, |R_*| — определитель матрицы парных корреляций, полученной после вычеркивания строки и столбца, представляющих связи зависимой переменной (Y).

В множественном регрессионном анализе исследуется связь между несколькими независимыми переменными (предикторами)  X₁, X_2,…X_m  и результативным признаком (откликом)  Y. Следовательно,

Y=f(X₁, X_2,…X_m) + ε.