Математическая постановка задачи оптимального проектирования цифровых фильтров. Основные типы фильтров частотной селекции и их применение, страница 8

В рамках данной структуры входной сигнал  предварительно проходит через фильтр дециматор с функцией передачи , который понижает частоту дискретизации в ν раз (максимальное значение коэффициента ν пропорционально отношению частоты дискретизации входного сигнала к ширине полосы пропускания входного фильтра). Формирующий фильтр с функцией передачи , работающий на пониженной в ν раз частоте дискретизации формирует заданную прямоугольность АЧХ проектируемого фильтра. Последующий фильтр интерполятор с функцией передачи , восстанавливает промежуточные отсчёты отфильтрованного сигнала  на выходе формирующего фильтра.

Рассмотрим пример  

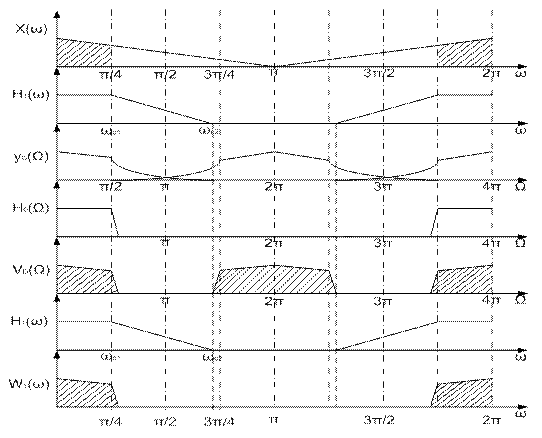
Недостатки метода.

1)  Потенциально достижимый выигрыш в уменьшении вычислительных затрат требует особой организации памяти данных с тем, чтобы операция копирования данных не приводила к большим временным затратам.

Проблема была решена разработкой полифазной формы фильтра-дециматора.

2)  В рамках одноступенчатой реализации по-прежнему требуется память данных большей ёмкости.

Решением этой проблемы связано с переходом к многоступенчатой реализации в виде последовательного соединения более простых фильтров.

Альтернативный метод предполагает использование параллельных форм фильтра-дециматора, в рамках которого в памяти данных сохраняются не входные отсчёты , а результаты промежуточной обработки и накопления последовательности отсчётов выходных данных .

3)  Шумы децимации и ошибки интерполяции вследствие неидеальности частотных характеристик фильтров.

2.11. Методы синтеза многоступенчатых структур узкополосных ЦФ.

1.Метод М. Белланже.

Идея метода заключается в построении фильтра – дециматора и фильтра – интерполятора в форме соединения предельно простых фильтров, каждый из которых понижает или, соответственно, повышает частоту дискретизации в 2 раза.

Т.о. общая структура фильтра принимает следующий вид:

Данная структура наиболее эффективна, когда ν_max = 2^m. Несмотря на то, что каждый последующий фильтр – дециматор имеет все более узкую полосу частот, в значениях приведенных частот все эти фильтры имеют однотипные характеристики. Так что увеличение показателя прямоугольности α в 2 раза от ступени к ступени компенсируется уменьшением в 2 раза показателя узкополосности β. Общие вычислительные затраты составят: 2N₁ + N/ν², где N₁=2L₁(ε_1доп, ε_2доп), N – порядок узкополосного фильтра, реализуемого обычным способом.

Полученное выражение показывает высокую эффективность данной структуры при синтезе узкополосных фильтров, т.е. когда ν>10.

Недостатки метода Белланже:

¨  если ν_max не кратно степени 2 (например ν_max=31), то фактическое значение ν_max = 16 и формирующий фильтр будет работать на относительно повышенной частоте дисретизации. Т.е. данная структура не дает оптимального решения с позиции минимизации относительных затрат.

¨  Подключение каждого последующего фильтра может привести к двойному увеличению неравномерности АЧХ в полосе пропускания. Поэтому приходится накладывать более жесткие требования на точность представления АЧХ каждого фильтра в полосе пропускания.

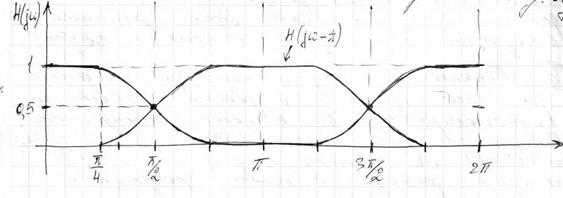
Полуполосные фильтры.

Полуполосный фильтр по определению Белланже представляет собой фильтр, ИХ которого удовлетворяет следующему требованию: h(2n) = 0,5 при n = 0 и h(2n) = 0 при n ≠ 0. Все свойства частотной избирательности фильтра определяются только нечетными отсчетами ИХ.

Свойсва полуполосных фильтров:

¨  Затраты на его реализацию уменьшаются фактически в 2 раза.

¨  Передаточная функция H(z) полуполосного фильтра отвечает равенству вида:

H(z)+H(-z)=1. т.о. если z=e^jw, то H(e^jw) + H(e^j(w-π) = 1, тогда характеристика принимает следующий вид:

2. Метод Крошье – Рабинера (оптимальный синтез многоступенчатых структур).

Идея подхода: синтез оптимальной многоступенчатой структуры, в рамках которой число ступеней фильтров – дециматоров (интерполяторов), а также конкретное значение  ν_i является неизвестным и рассчитывается по критерию минимума ячеек памяти данных.

Структура фильтра:

Каждый фильтр имеет свои параметры N_i и ν_i.

3. Структура с параллельными накопителями.