Математическая постановка задачи оптимального проектирования цифровых фильтров. Основные типы фильтров частотной селекции и их применение, страница 13

Значительное уменьшение общих вычислительных затрат в рамках представленной двухкаскадной структуры можно добиться путем использования параллельного набора из 3, 4, 5, … ГФ. При этом увеличивается период следования боковых полос функции передачи каждого ГФ, а значит пропорционально расширяется переходная зона АЧХ последующих сглаживающих фильтров и значит уменьшается порядок последнего.

Другой путь повышения эффективности состоит в том, что набор СФ может строиться по многокаскадной структуре. При этом общая схема соединений принимает пирамидальный вид.

В классе БИХ-цепей:

Двухкаскадная структура полосового фильтра имеет вид:

Приведенная структура полосового БИХ-фильтра отличается существенным снижением чувствительности частотных характеристик фильтров к неточному представлению коэффициентов, т.к.:

• ЦГФ, отличаясь воспроизведением с заданной высокой прямоугольностью АЧХ проектируемого фильтра, фактически синтезируется как базовый НЧФ, у которого вместо элемента задержки z^-1  стоит z^-υ. При этом у базового НЧФ полоса пропускания расширяется пропорционально υ, а следовательно существенно уменьшается чувствительность характеристик (в υ^М раз, где М – порядок БИХ-фильтра).
• Значительное расширение полосы пропускания и переходной зоны АЧХ СФ по отношению к узкополосному проектируемому фильтру, что снижает порядок фильтра и увеличивает расстояние между полюсами передаточной функции.

Пример:

Пусть проектируется фильтр Баттерворта со следующими параметрами частотной избирательности:

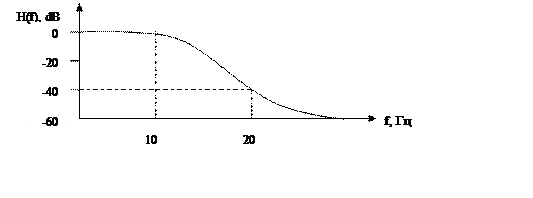
Расчет показывает, что требуемый порядок фильтра составляет М ≥ 7. Требуемая разрядность представления коэффициентов q > 54 двоичных единицы, чтобы обеспечить сохранение полюсов внутри единичного круга.

Для реализации требуемой частотной избирательности в рамках рассмотренной выше двухкаскадной структуры воспользуемся двумя фильтрами со следующими параметрами частотной избирательности:

1. базовый НЧФ – фильтр Баттерворта 7 порядка. На частоте F_c11 = 10 Гц затухание: - 3 дБ, на частотах выше F_c21 = 20 Гц затухание: - 40 дБ. При этом частота дискретизации базового фильтра: 400 Гц. Коэффициент прореживания ИХ: υ=25.
2. сглаживающий фильтр – фильтр Баттерворта 3 порядка. При этом на частоте F_c12 = 80 Гц затухание: - 3 дБ, на частотах выше F_c22 = 380 Гц затухание: - 40 дБ.

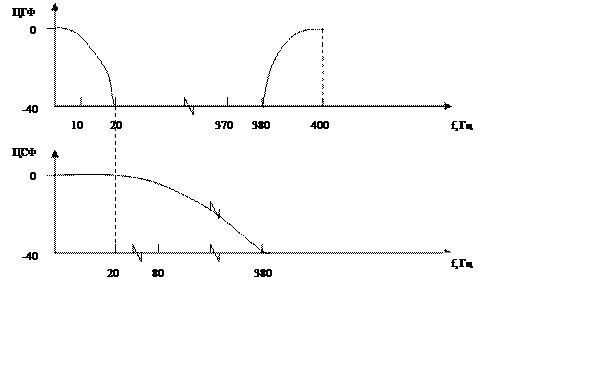
Расчет требуемой точности представления коэффициентов фильтра показывает, что для ЦГФ: q ≥ 18 двоичных единиц, для ЦСФ: q ≥ 14 двоичных единиц.

Отметим, что в данном примере коэффициент прореживания ИХ υ=25 выбирался эмпирически (без оптимизации). С целью оптимизации структуры следует несколько увеличить параметры υ, при этом базовый НЧФ станет менее узкополосным, что позволит уменьшить требуемую точность представления его коэффициентов. Вместе с тем, СФ будет иметь более узкую переходную зону АЧХ, а следовательно возрастет его порядок, и как следствие, требуемая разрядность представления коэффициентов. Очевидно при υ = υ _опт можно добиться значения q_ЦГФ = q_ЦСФ = 16 двоичных единицы.

2.18  Построение набора цифровых полосовых фильтров с прореживанием по частоте: пирамидальная структура.

В классе КИХ-цепей:

М=8.

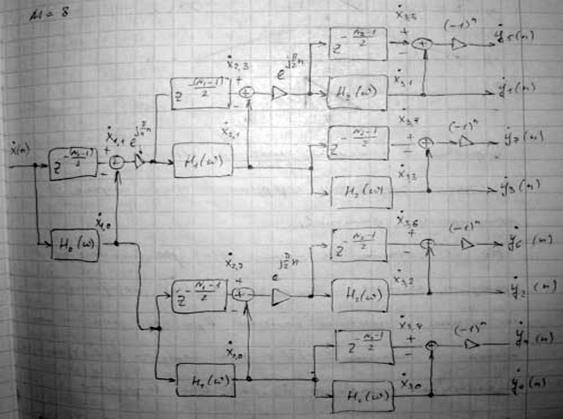
Рассмотрим преобразование спектра входного сигнала при выделении 4-ого частотного канала

(у₄ (n)).

Цифровая 8 канальная система частотной селекции включает 3 ступени преобразования и содержит в общем случае 7 полуполосных фильтров.

На 1 ступени входной сигнал x(n) расщепляется на 2 последовательности данных: x_1,0(n) и x_1,1(n), содержащих соответственно четные и нечетные каналы. При этом достаточно использовать только 1 полуполосный ГФ с функцией передачи Н₀(ω), непосредственно выделяющей составляющую x_1,0(n). Для выделения x_1,1(n) достаточно воспользоваться свойствами антисимметричности ИХ полуполосного фильтра. Полученную на его выходе последовательность x_1,0(n) вычесть из входного сигнала x(n), задержанного на половину длины импульсной характеристики полуполосного ГФ с функцией передачи Н₀(ω).