Во втором случае частота дискретизации остатка предсказания уменьшается в 3 раза (γ=3) т.е. принимает значение 2,4 кГц.
Кодер RELP более устойчив к воздействию помех.
![]()

Кодер с многоимпульсным возбуждением.
Классический LPC кодер с возбуждением от основного тона (шума с заданной интенсивностью) не обеспечивают необходимого качества синтезир. речи т.к. не для всех звуков удается получить точное разделение речи на вокализованные и не вокализованные. Кроме того известно, что помимо основного возбуждения в более точной модели речеобразования имеется вторичное возбуждение, следовательно можно предполагать, что возбуждение локализованной речи должно состоять из нескольких импульсов в течении периода основного тона.
Основное преимущество много импульсного возбуждения состоит в том, что оно определяет возбуждение для любого речевого сегмента, при этом не требуется продв. значение не овокализованных данных сегмента, не о о периоде основного тона. Много импульсное возбуждение представляется в виде последовательности импульсов V(n) с непрерывно распределенными интервалами и различными амплитудами (примерно 8 импульсов за 10 мс). Амплитуды и расположение импульсов определяется путем используемой процедуры Анализ через синтез.
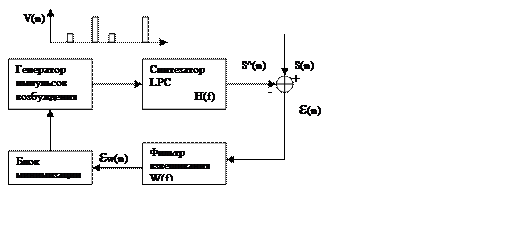
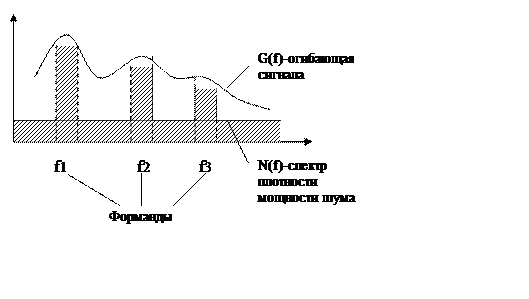
Фильтр взвешивания с периодической функцией W(f) подавляет шум в промежутках между форматными областями и тем самым как бы подчеркивает формантныеобласти над шумом.
Взвешенное значение ошибки εw(n) минимизируется путем оптимизации местоположения и амплитуд импульсов сигнала возбуждения V(n), при этом оптимальное местоположение определяется для каждого импульса в отдельности, начиная с первого.
Пусть mi и gi, i от 1 до k временное положение и амплитуда i-го импульса на периоде основного тона.
Выражение для взвешенной мощности остатка предсказания между исходным и синтезированными речевыми сигналами имеет вид:

h(n)-импульсная характеристика синтезирующего фильтра
Процесс определения местоположения импульсной и их амплитуд продолжается до тех пор пока ошибка Ew не уменьшится до приемлимого значения, установлено, что после размещения 8-ми импульсов в интервале
10 мс дальнейшие уменьшение сигнала остатка происходит не значительно.
Кодер с кодовым возбуждением CELP.
В этом случае сигнал возбуждения представляется в виде вектора, которому присваивается индекс-адрес в кодовой книге. Выбор оптимального кодового вектора производится из большого множества векторов, кандидатов, которые образуют кодовую книгу. При этом требуется производить достаточно большой объем вычислений, что является основной проблемой данного кодека.
Метод линейной спектральной пары LSP.
Коэффициенты ai, i от 1 до M предскпзания обладают широким динамическим диапазоном, это затрудняет их эффективное квантование т.е. требует большой разрядности представления, в случае ограниченной разрядности и воздействии искажения со стороны КС может привести к неустойчивой работе синтезир. LPC фильтров на приемной стороне, т.к они являются БИХ фильтрами.
В 1979 г. Итакура предложил новый метод определения параметров характер. огибающую спектра речи, этот метод назвали методом линейной спектральной пары. Предложенный метод в математическом смысле полностью эквивалентен обычному описанию фильтра с линейным предсказанием, но более устойчив к ошибкам в КС, при этом искажения одного LSP параметра влияет на спектор речи только в определенной области частот, в то время как искажение коэффициентов ai распространяется на всю область частот.
Параметры LSP получаются из коэффициентов LPC разложением передаточной функции фильтра анализа A(Z), на сумму двух полиномов, это может быть выполнено с помощью коэффициентов передачи прямого и обратного фильтра.
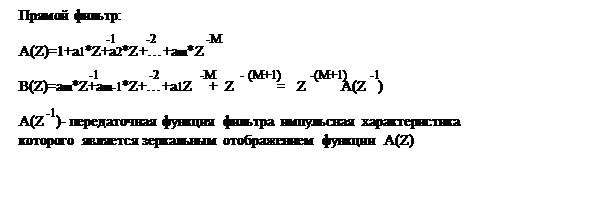
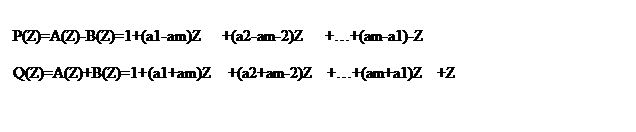 Представленное
выражение используется для формирования следующих полиномов:
Представленное
выражение используется для формирования следующих полиномов:

Анализ данных выражений показывает, что все корни полиномов P(Z) и Q(Z) лежат на единой окружности в Z области и чередуется с увеличением частоты.
Можно показать что:


Частные параметры ωpi, ωqi являются параметрами линейной спектральной пары, которые располагаются на линейной спектральной окружности, при этом соблюдаются следующие условия:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.