Заметим, что спектр сигнала x1,1(n) отличается от спектра сигнала x1,0(n) сдвигом по частоте частотных каналов на Δω=π/4, поэтому если выполнить трансформацию спектра сигнала x1,1(n) на величину Δω=π/4, то последующая его обработка будет аналогичной обработке сигнала x1,0(n).
Нетрудно увидеть (см. схему), что на второй ступени преобразования описанная выше структура алгоритма разделения частотных каналов на четные и нечетные повторяется для каждой из двух входных последовательностей. А на третьей ступени преобразования для окончательного разделения двух оставшихся полос используются предельно простые полосовые СФ с функцией передачи Н2(ω), которая также отвечает свойству полуполосности.
Оценим затраты на реализацию этой структуры. Вычислительные затраты складываются из двух составляющих – 1) затраты на квадратурную комплексную модуляцию;
2) затраты, связанные с реализацией полуполосных ГФ.
VПФ=2*М*(1+1/2+1/4+...+2/M) + Σ 2i * Ni/υi , где m=log2M, Ni и υi – порядок i-ого полуполосного ГФ и коэффициент прореживания его ИХ.
Поскольку на последующей ступени преобразования вместо операции умножения используется операция (-1)n, а на предыдущей ступени преобразования фактически выполняется умножение на комплексную величину вида: 1+j*0; -1+j*0; 0+1*j; 0-1*j, то общие затраты на модуляцию равны М.
Отметим, что отношение Ni/υi= N0/υ0 для i от 1 до m-1, так как на каждой последующей ступени преобразования с одной стороны коэффициент прореживания υi уменьшается в 2 раза, а с другой стороны Ni тоже уменьшается в 2 раза, так как в 2 раза расширяется переходная зона АЧХ.
Можно показать, что υ0 определяется соотношением
υ0=М/2
следовательно, Ni/υi= 2*N0/М.
VПФ=М + 2*N0/М *(1+2+4+...+M/2)= М + 2*N0/2*(1+1/2+1/4+...+2/M)=M+2*N0≈2*N0 (при N0>>M)
Вывод: общие затраты не зависят от числа каналов при N0 >> M
В классе БИХ-цепей:
Рассмотрим построение набора из М полосовых БИХ-фильтров с однотипными ЧХ:
М=8
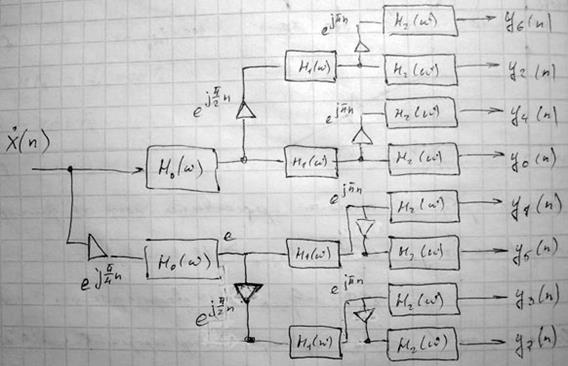
В рамках данной пирамидальной структуры каждая ветвь, соединяющая некоторый вход с некоторым к-ым выходом (к = от 0 до 7) включает одну и ту же последовательность элементарных ЦГФ, которая заканчивается наипростейшим СФ, имеющим как правило 3 порядок. Отличие состоит в использовании соответствующей каждому выходному каналу последовательности квадратурных модуляторов.
Общее описание и методы синтеза.
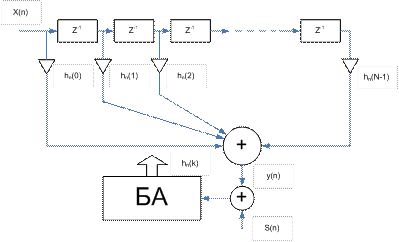
С целью вывода алгоритма адаптации перейдем от прямой формы свертки отсчетов входного сигнала X(n) и коэффициентов h(k) к векторно-матричной форме представления:
, где 
, 
(5.1)
(5.2)
Мгновенное значение квадрата ошибки:
Пусть 
, S(n) и X(n) – стационарные
эргодические случайные процессы. Найдем средний квадрат отклонения(СКО),
представляющий собой мат. Ожидание квадрата ошибки. При этом будем полагать,
что на текущем шаге адаптации коэффициенты фильтра принимают постоянное
значение.
(5.3)
- корреляционная матрица размером N*N отсчетов
входного сигнала
- транспонированный вектор взаимной корреляции
обучающего и входного сигнала.
(5.3) фактически описывает так называемую рабочую функцию, определяющую зависимость СКО от выбранного вектора коэффициентов h.
Из (5.2) следует, что если отсчеты входного и обучающего сигнала – стационарные случайные процессы, то рабочая ф-я является квадратичной, при этом СКО, как квадратичная функция имеет только один глобальный оптимум, который легко установить, найдя градиент СКО и приравняв его к 0.
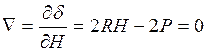(5.4)
Из (5.4) =>
(5.5)
Подставив (5.5) в (5.3) получим минимальное значение СКО в точке глобального оптимума.
Принимая во внимание, что матрица R является квадратичной и симметричной, т.е.
, а так же используя правило преобразования
матр. произведений и тот факт, что каждой из трех составляющих, входящих в
данное выражение, можно показать, что
(5.6)
Анализ выражений (5.5) и (5.6) показывает:
Адаптивная ф-я возможна только при наличии взаисной корреляции входного и обучающего сигнала (а противном случае, если p=0, то Hopt=0).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.