2. Выходные ступени преобразователя используют всё большее количество фильтров с возрастающим числом ячеек памяти данных и соответствующей крутизной частотных характеристик , но при этом чем дальше от входа по пирамиде тем всё более уменьшается частота дискретизации входных сигналов а значит уменьшаются требования к скорости обработки и уменьшается память данных каждого отдельного фильтра .
Полифазная форма с применением ДПФ

В рамках данной структуры разделение входного сигнала mT1 на M – субполосных составляющих выполненных с помощью M- точечного ДПФ , спектральное окно которое формируется входным фильтром дециматором реализованным по полифазной структуре . Т.о. вместо M- полосовых фильтров демодуляторов реализуется только один НЧ-фильтр , полифазная составляющая на входе которого преобразована с помощью ДПФ в M- субполосных составляющих . Если M кратно степени двойки то используется алгоритм БПФ. Следовательно суммарные затраты уменьшаются пропорционально числу каналов.
Прямая параллельная форма синтеза набора ЦФДМ

Для реализации набора из N- фильтров демодуляторов порядка N , предварительно используют 2N – точечное ДПФ , для каждой i-й субполосы формируется спектр (набор коэф. Фурье соотв. Спектру сигнала на выходе i-го фильтра демодулятора путём простого перемножения коэф. Фурье входного сигнала на коэф. Фурье частотной характеристики i-го субполосного фильтра ) С тем чтобы выделить комплексную огибающую i-й субчастоты производится трансформация коэф. Фурье i-й субполосы в НЧ-область.
Эффект уменьшения в ![]() раз частоты дискретизации реализуется
путём выделения только 2N/
раз частоты дискретизации реализуется
путём выделения только 2N/![]() коэф. Фурье i-го
субполосного сигнала с последующим их периодическим повторением , с периодом 2/
коэф. Фурье i-го
субполосного сигнала с последующим их периодическим повторением , с периодом 2/![]() .
.
Для формирования самого
субполосного сигнала i-й субполосы используется ОДПФ размерностью 2N/![]() .
.
Выигрыш :-существенное уменьшение затрат достигается за счет :
1.Для реализации линейной свёртки каждого частотного канала используется алгоритм двойного БПФ
2.Т.к. для всех каналов используется один и тот же входной сигнал то ППФ выполняется только один раз
3.Для уменьшения вычислительных
затрат в ![]() раз при реализации ОДПФ используется
усечение коэф. Фурье . Т.о. для каждого канала выполняется ОДПФ размерностью 2N/
раз при реализации ОДПФ используется
усечение коэф. Фурье . Т.о. для каждого канала выполняется ОДПФ размерностью 2N/![]() .
.
Недостаток - усечение истинного спектра сигналов на выходе фильтра демодулятора за пределами основной полосы пропускания , поэтому данный метод применяется для высокоизбирательных фильтров , когда ступень затухания в зоне непрозрачности 80дБ и более.

Цифровой фильтр называется гребенчатым, если в рабочем диапазоне частот от 0 до 2π:
![]() - его частотная
характеристика
- его частотная
характеристика
![]()
H(jω) является
периодичной функцией с периодом ![]() , где ν – целое число.
, где ν – целое число.
Рассмотрим основные характеристики и свойства ЦГФ.
Периодический характер частотной характеристики ЦГФ обуславливает "прореженность" его импульсной характеристики:
 при
при 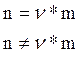 (1)
(1)
![]() - импульсная характеристика
базового ФНЧ, работающего на пониженной в ν раз частоте дискретизации.
- импульсная характеристика
базового ФНЧ, работающего на пониженной в ν раз частоте дискретизации.

![]()
Заметим, что в соответствии с (1) импульсная характеристика ГФ может быть получена из импульсной характеристики базового ФНЧ путём простого добавления ν-1 нулей между каждой парой соседних отсчетов.
Установим связь между передаточными функциями ЦГФ и базового ФНЧ:
 (2)
(2)
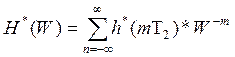 - передаточная функция базового
ФНЧ.
- передаточная функция базового
ФНЧ.
Т.о. в соответствии с (2) передаточная функция ЦГФ связана с
передаточной функцией базового ФНЧ отображением вида ![]()
Представим иллюстрации преобразования импульсных и частотных характеристик при переходе от базового ФНЧ к ЦГФ, ν=4:
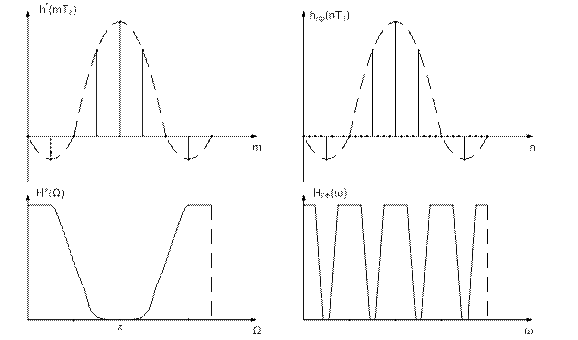
Гребенчатые КИХ-фильтры.
Для гребенчатого КИХ-фильтравходы и выходы связаны друг с другом сверткой вида:

С учётом формулы (1) получим:
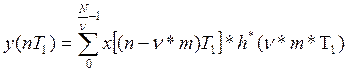 (3)
(3)
Вычислительные затраты на реализацию свертки в форме (3) уменьшается в ν раз. Заметим, что при этом память фильтра определяется порядком N. Общая структурная схема фильтра принимает вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.