Математическая постановка задачи оптимального проектирования цифровых фильтров. Основные типы фильтров частотной селекции и их применение, страница 7

Для вычисления коэффициента Фурье требуется N² операций комплексного умножения с накоплением. Тригонометрический базис обладает свойствами периодичности на интервале от 0 до N-1, что позволяет сократить объем вычислительных затрат.

Основная идея алгоритма БПФ состоит в том, чтобы разбив исходную N-точечную последовательность на 2 более короткие (N/2 и N/2) и выполнив для каждой из них N/2-точечное БПФ восстановить N-точечное БПФ при минимальных дополнительных затратах. В этом случае общие затраты составляют N²/2, т.е. в 2 раза меньше, чем вычисление N-точечного БПФ. При N кратном степени 2 общие затраты будут N∙log₂N.

Алгоритм БПФ можно показать используя модификацию прореживания по времени. Исходная последовательность x(n) делится на четные и нечетные отсчеты. Затем заменяются индексы суммы n = 2r для четной и n = 2r + 1 для нечетной последовательностей:

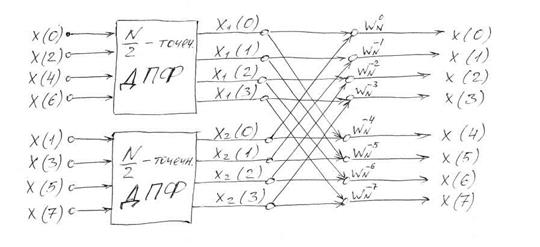
Из последней формулы видно, что для объединения двух N/2-точечных БПФ в одно N-точечное требуется дополнительно N операций умножения. Т.к. при N>10 N<<N², то этими затратами можно пренебречь. Недостающие X₁(k) и X₂(k) при k ≥N/2 получают путем простого периодического продолжения. Для N=8 графически алгоритм БПФ можно изобразить так:

Одним из самых распространенных применений ДПФ, помимо цифрового спектрального анализа, является реализация на его основе высокоскоростной свертки по алгоритму прямого и обратного БПФ. Алгоритм быстрой свертки включает в себя следующую последовательность операций:

1.         Секционирование отсчетов входной последовательности .

Введем новые последовательности

 

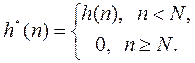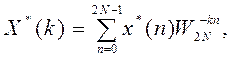2.         Прямое ДПФ -мерных последовательностей

 

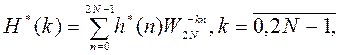(3)

 

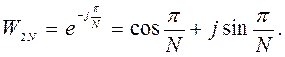где

3.         Перемножение Фурье-образов

(4)

4.         Обратное ДПФ -мерной последовательности коэффициентов Фурье

 

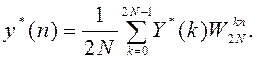(5)

5.         Накопление (в памяти) отсчетов выходной последовательности для всех  и отбрасывание отсчетов  для всех .

Если  и, соответственно , кратны степени 2, то прямое (3) и обратное (5) ДПФ можно вычислить по алгоритму БПФ, затратив на каждое преобразование  операций умножения и сложения действительных чисел (вместо  для обычного ДПФ). Общие вычислительные затраты на реализацию свертки по алгоритму двойного БПФ, с учетом (4), составят

 

или, в пересчете на один выходной отсчет ,

 

вместо  операций для прямого метода.

Таким образом, для всех  и кратных степени 2, более эффективным в вычислительном отношении является метод двойного отображения на основе алгоритма БПФ.

2.10. Метод синтеза структуры узкополосного ЦФ на основе децимации и интерполяции.

Идея метода состоит в последовательном подключении друг к другу фильтра дециматора и фильтра интерполятора, функция передачи которых  – , определяется  свойствами частотной избирательности проектируемого узкополосного фильтра, при этом одноступенчатая реализация принимает вид:

В рамках данной структуры дециматор практически выполняет роль узкополосного НЧ фильтра, вычисляющего каждый ν-тый отсчёт выходного сигнала, а следовательно при реализации в классе КИХ-цепей требует в ν раз меньшего объёма вычислений.

Для восстановления «пропущенных» отсчётов выходной сигнал y(nT1) используется интерполятор. Вычислительные затраты которого также в ν раз меньше по  отношению к обычной форме реализации узкополосного фильтра. Т.о. общий объём вычислений уменьшается в ν/2 раз. Т.о. эффективность данной структуры растёт пропорционально коэффициенту ν, значение которого определяется отношением частоты дискретизации входного сигнала к ширине полосы пропускания фильтра, т.е. коэффициент ν прямо пропорционален показателю узкополосности фильтра β.

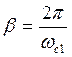
Данная структура является предельно эффективной в тех случаях, когда коэффициент прямоугольности АЧХ  . В тех же случаях, когда  используют следующую структуру, аналогичную предыдущей, но включающую между дециматором и интерполятором формирующий фильтр, который и определяет прямоугольность АЧХ, представленной структуры, которая принимает следующий вид: