Другие предметы \ Цифровая обработка сигналов

Математическая постановка задачи оптимального проектирования цифровых фильтров. Основные типы фильтров частотной селекции и их применение, страница 5

Этот класс состоит из цепей, для которых входной  и выходной сигналы удовлетворяют линейному разностному уравнению с постоянными коэффициентами.

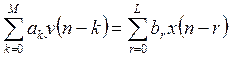
 - постоянные коэффициенты.

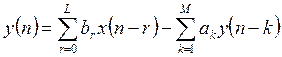
Как и в случае свертки это выражение дает не только строгое математическое описание оператора F, но может быть использовано для непосредственной реализации ЦФ. Данный класс называется классом БИХ – цепей. Отметим, что L<<N и M<<N

Если цепь описана линейным разностным уравнением в такой форме, то ее передаточная функция является отношением полиномов.

Используя Z-преобразование левой и правой части и вводя , , получим:

Используя подстановку  получим выражение для функции передачи цепи, т.е. его комплексной частотной характеристики:

Фактически это выражение задает пространство строго воспроизводимых функций передачи в классе БИХ цепей заданного порядка.

Сформулируем задачу минимаксной аппроксимации для класса БИХ.

Пространство , где D=M+L+2 строго воспроизводимых  функций передачи в классе БИХ цепей задается следующим представлением:

- D-мерный вектор коэффициентов цифровой цепи.

Цель оптимального синтеза БИХ цепи связана прежде всего с решением задачи аппроксимации  АЧХ-цепи, которая сформулирована следующим образом.

Найти минимальный порядок D и вектор коэффициентов  такие, при которых для заданной меры отклонения  имеет место неравенство вида

Решение этого неравенства связано с решением 3-х проблем:

  1. Корректности самой постановки задачи;
  2. Поиска эффективных методов приближения к дробно-рациональным функциям.
  3. Проблема физической реализуемости и устойчивости.

В силу сложности прямого решения задачи аппроксимации в инженерной практике широко используют косвенные методы, которые дают решения, близкие к оптимальным.

На частотном этапе синтеза производится расчет параметров эквивалентного по свойствам частотной избирательности задающим характеристики аналогового фильтра  прототипа с , при этом используют хорошо отработанный аппарат фильтров класса:

  • Бесселя;
  • Баттероворта;
  • Чебышева (1 и 2 рода);
  • Золоторева;
  • Эллиптичности.

На 2-м этапе используя билинейное преобразование переходят к цифровому фильтру с .

2.7. Методы построения цифровых фильтров в классе КИХ цепей.

Известно 3 основных подхода к построению структур ЦФ в классе КИХ цепей:

  Линейная свертка и ее модификации.

  Интерполяция передаточной функции передачи цепи.

  Двойное отображение с использованием быстрых алгоритмов перехода из временной области в обобщенную частотную область и обратно.

ТЧП – теоритекочисловые преобразования.

Линейная свертка предполагает реализацию по прямой форме вида

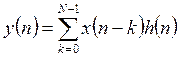 или в виде каскадного или параллельного соединения КИХ звеньев более низкого порядка.

Многоскоростная фильтрация является дальнейшим развитием эффективной реализации систем цифровой и частотной селекции сигналов с использование эффектов прореживания по времени и по частоте, которые предполагают каскадную форму реализации линейной свертки.

При реализации свертки в прямой форме с импульсной характеристикой  воспроизводимая передаточная функция принимает вид: 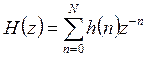, то есть является полиномом N-го порядка, а значит может быть аппроксимирована, например с помощью интерполяционных  формул Лагранжа, Ньютона, Тейлора и т.д. На практике нашел применение частный случай  интерполяции по Лагранжу – метод частотной выборки.

Структура КИХ фильтра N-го порядка на основе этого метода  частотной выборки строится путем каскадного соединения  элементарного гребенчатого фильтра N-го порядка вида:

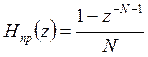, формирующего N+1 нулей, равномерно распределенных по единичной окружности и параллельного набора цифровых резонаторов на основе БИХ звеньев 1-го порядка с комплексными коэффициентами, формирующими N+1 полюсов, положение которых совпадает с  положением нулей передаточной функции гребенчатого фильтра.

Существует 2 принципиальных преимущества метода частотной выборки:

  При синтезе узкополосного фильтра, когда реальное число резонаторов существенно меньше порядка фильтра N.

Скачать файл