Математическая постановка задачи оптимального проектирования цифровых фильтров. Основные типы фильтров частотной селекции и их применение, страница 28

На практике, приемное устройство и антенны вносят во входные сигналы независимые шумы. Эти шумы оказывают значительное влияние на работу системы. С тем, чтобы в рассмотренной выше схеме подавлялась направленная помеха, но не подавлялся полезный сигнал, помеха должна быть мощной, а сигнал слабым по сравнению с шумами приемника.

Схема устройства подавления боковых лепестков (помехи) при приеме одного сигнала заданной частоты:

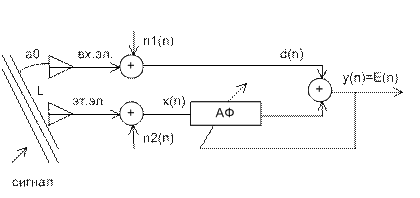
Задача состоит в построении устройства подавления сигнала по одному из направлений, например для , и передачи без искажений в остальных направлениях. Ненаправленные антенны разнесены на расстояние . Предполагается, что принимается единственный сигнал, поступающий под углом .

Пусть составляющая сигнала на входном элементе принимает вид:

Составляющая сигнала на эталонном элементе:

- это число отсчетов опережения фазового фронта сигнала .

При отсутствии шума приемника весовые коэффициенты адаптивного фильтра приемника настраиваются так, что сигнал подавляется полностью, однако, при наличии шума, как будет показано далее, подавление сигнала не происходит и устройство работает удовлетворительно.

Для анализа этой ситуации рассмотрим схему настройки устройства подавления для направленного приема сигнала под углом (а) и ее упрощенный вариант для определения ДН устройства подавления после его адаптации (б).

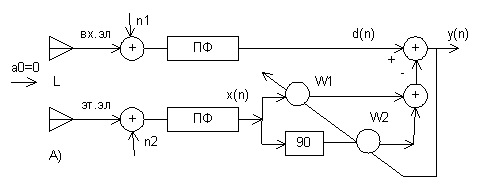
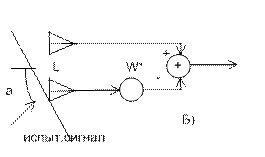
Будем считать, что каждый из полосовых фильтров имеет единичный коэффициент передачи на центральной частоте полосы пропускания . Для регулирования амплитуды и фазы сигнала частоты  адаптивный фильтр должен иметь синфазный и квадратурный весовые коэффициенты W1 и W2.

Предположим, что шумы приемника n1 и n2 являются независимыми друг от друга, в том числе относительно составляющих сигнала. -мощность каждого из них в полосе пропускания полосового фильтра.

Вычислим автокорреляционную функцию эталонного сигнала x(n) и ВКФ между эталонным x(n) и входным d(n) сигналами для произвольного угла прихода . Можно показать, что оптимальные значения весовых коэффициентов принимают вид:

Если  и оптимальный вектор коэффициентов:

В этом случае ОСШ на входе адаптивного фильтра можно определить как отношение мощности входного или эталонного сигнала к мощности шума приемника в полосе пропускания следующим образом:

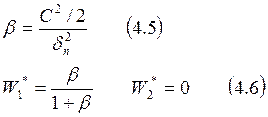
Из представленной выше схемы с учетом выражений (4.1) и (4.4) можно найти выражение для выходного сигнала:

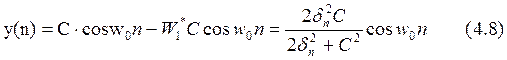
Из приведенного анализа видно, что при слабом по сравнению с шумом приемника входном сигнале s(n) ОСШ  мало и следовательно, значение весового коэффициента  W1 будет стремиться к 0. В этом случае выходной сигнал y(n) приблизительно совпадает с сигналом s(n), т.е. сигнал почти не подавляется; однако, при мощном сигнале s(n) >>1, W1 стремится к 1, т.о. выходной сигнал y(n) стремится к 0, т.е. происходит значительное подавление сигнала (помехи).

Если угол прихода  не равен 0, то имеет место соотношение (4.3), т.е. весовой коэффициент W2 не стремится к 0, а коэффициент W1 принимает отличное от (4.6) значение, вместе с тем, амплитуда выходного сигнала определяется по-прежнему выражением, аналогичным (4.8).

Представляет интерес определение чувствительности приемной системы для всех остальных углов , при условии . Подобную зависимость называют ДН.

Пусть после адаптации к сигналу, приходящему по нулевому направлению, весовые коэффициенты имеют значение, соответствующее (4.6). Далее будем полагать, что испытательный сигнал на частоте  приходит под углом  и , а соответствующие составляющие испытательного сигнала на входном элементе:

Тогда составляющие сигнала на эталонном элементе:

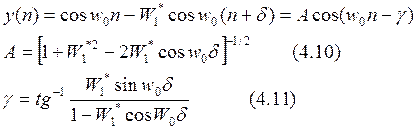
Тогда, коэффициент передачи решетки принимает следующее значение:

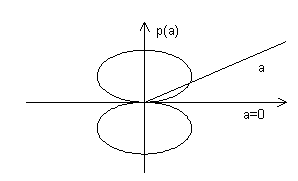Отметим, что коэффициент передачи по мощности P принимает минимальное значение при , т.к. при  . Это равносильно пространственной режекции в направлении прихода первоначального сигнала. При этом, чем мощнее был настроечный сигнал, тем выше уровень режекции. По мене роста ОСШ  происходит быстрое увеличение уровня адаптивной режекции, и выходной сигнал стремится к 0. При значениях  коэффициент передачи ДН возрастает, при этом ДН принимает следующий вид:

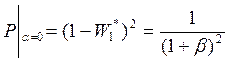
Выводы:

1)  Рассмотренное устройство работает нормально тогда, когда полезные входные сигналы   являются слабыми, а помехи – сильными ( по отношении к шуму приемника)