Под оптимальным проектированием цифровой цепи будем понимать, как видно из описания, такое проектирование, которое предполагает не просто поиск оператора, обеспечивающего воспроизведение желаемой функции передачи с заданной точностью, но прежде всего поиск наилучшей в смысле принятого критерия качества структуры цели, включая оптимизацию всех ее параметров.
Рассмотренная выше математическая постановка задачи является достаточно общей и требует конкретизации всех соотношений входящих в формулировку задачи. Возникающие здесь вопросы можно разделить на три группы:
описание и формализация
класса операторов GF обеспечивающих воспроизведение желаемой функции передачи ![]() с наперед заданной точностью
с наперед заданной точностью ![]() в метрике пространства R;
в метрике пространства R;
описание и формализация подклассов ![]() в классе операторов GF, представление целевой функции
в классе операторов GF, представление целевой функции ![]() и вектора граничных условий
и вектора граничных условий
![]() в подклассах
в подклассах ![]() в
классе операторов GF.
в
классе операторов GF.
Рассмотрим постановку и решение задачи аппроксимации с желаемой функцией
передачи ![]() . Желаемую функцию передачи полосового
фильтра представим в виде:
. Желаемую функцию передачи полосового
фильтра представим в виде:
|
|
где ![]() — Центральная частота
полосы пропускании,
— Центральная частота
полосы пропускании, ![]() и
и ![]() частоты
среза полосы пропускания и зоны непрозрачности; k — параметр, определяющий постоянную задержки.
частоты
среза полосы пропускания и зоны непрозрачности; k — параметр, определяющий постоянную задержки.
Таким образом, будем полагать, что идеальная комплексная частотная характеристика цифрового фильтра частотной селекции должна иметь строго линейную ФЧХ, обеспечивать единичный' коэффициент передачи в полосе пропускания и быть абсолютно непрозрачной в области частот возможного появления помехи.
|
где р(ш) —весовая функция, принимающая значения |
Представление желаемой частотной
характеристики в пространстве R строго
воспроизводимых в классе ![]() функций передачи
функций передачи ![]() является по существу
задачей аппроксимации и предполагает заданной метрику
является по существу
задачей аппроксимации и предполагает заданной метрику ![]() пространства
R. В теории цепей общепринятой является минимаксная аппроксимация, решающая задачу чебышевского приближения с
метрикой вида
пространства
R. В теории цепей общепринятой является минимаксная аппроксимация, решающая задачу чебышевского приближения с
метрикой вида
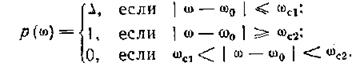
![]() - весовая функция, которая обычно
принимает вид:
- весовая функция, которая обычно
принимает вид:
|
Параметр |
![]()
Пространство ![]() строго воспроизводимых функций передачи
строго воспроизводимых функций передачи ![]() в классе КИХ цепей задается следующим
дискретным представлением:
в классе КИХ цепей задается следующим
дискретным представлением: 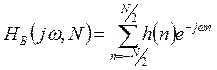
Для цифровых фильтров с линейной
ФЧХ на импульсную характеристику ![]() накладывают
дополнительные ограничения вида
накладывают
дополнительные ограничения вида ![]() , при этом
, при этом ![]() принимает вид
принимает вид
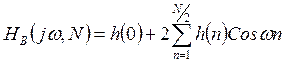 -
описывает функцию передачи фильтра с нулевой ФЧХ. Переход к физически
реализуемому фильтру приводит к тому, что функция передачи (по крайней мере
амплитудное значение) сохраняет свою форму, а ФЧХ – линейна.
-
описывает функцию передачи фильтра с нулевой ФЧХ. Переход к физически
реализуемому фильтру приводит к тому, что функция передачи (по крайней мере
амплитудное значение) сохраняет свою форму, а ФЧХ – линейна.
Т.о. если желаемая ЧХ ![]() может быть представлена на интервале
периодичности
может быть представлена на интервале
периодичности ![]() частичной суммой ряда Фурье,
размерность которой не превышает порядка цепи N, то
такая ЧХ принадлежит пространству строго воспроизводимых функций передачи
частичной суммой ряда Фурье,
размерность которой не превышает порядка цепи N, то
такая ЧХ принадлежит пространству строго воспроизводимых функций передачи ![]()
Представление с наперед заданной
точностью желаемой ЧХ не принадлежащей пространству ![]() имеет
место для всех функций
имеет
место для всех функций ![]() , отвечающим условиям теоремы
Вейерштрасса: для
, отвечающим условиям теоремы
Вейерштрасса: для ![]() непрерывной на интервале
периодичности
непрерывной на интервале
периодичности ![]() четной функции
четной функции ![]() и
и ![]() значения
значения
![]() найдется такое N-мерное
пространство
найдется такое N-мерное
пространство ![]() строго воспроизводимых функций передачи,
для которого при всех M>=N будет
иметь место следующее неравенство:
строго воспроизводимых функций передачи,
для которого при всех M>=N будет
иметь место следующее неравенство:
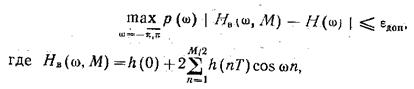
С учетом изложенного задачу аппроксимации в классе КИХ цепей можно сформулировать в следующем виде:
Найти минимальный порядок N и импульсную характеристику ![]() ,
отвечающую критерию близости к функции в смысле минимаксной аппроксимации
обеспечивающей воспроизведение желаемой функции передачи
,
отвечающую критерию близости к функции в смысле минимаксной аппроксимации
обеспечивающей воспроизведение желаемой функции передачи ![]() с ошибкой, не превышающей
с ошибкой, не превышающей ![]()
Решение задачи аппроксимации опирается на использование теоремы Чебышева о равноволновой аппроксимации и алгоритм замены Ремеза.
С целью уменьшения общих затрат,
связанных с реализацией ЦФ, воспроизводящего желаемую ![]() с
заданной точностью
с
заданной точностью ![]() используют класс линейных
операторов
используют класс линейных
операторов ![]() более общего вида.
более общего вида.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.