0<ω1<ω2<ω3<…<ωm<π
это условие необходимо и достаточно, для обеспечения стабильности работы синтезирующего фильтра.
Субполосное кодирование с векторным квантователем
(матричное кодирование).

Набор полосовых фильтров демодулятора разбивает спектр речевого сигнала на М полос и формирует М канальных сигналов, с понижением частоты дискретизации в М раз. На выходе каждого канала производится анализ на основе LPC метода с последующим векторным квантованием LPC параметров и сигналов возбуждения.
Достоинства:
1.Существенно уменьшается размерность кодовой книги, а значит поиск вектора параметров в кодовой книге.
2.Упрощается реализация фильтров с линейным предсказанием и соответствующих синтезирующих БИХ фильтров на приемной стороне.
3.Повышенная степень сжатия за счет эффективного сочетания потенциальных возможностей полосных вокодеров и вокодеров на основе LPC методов.
3.13. Векторное квантование при кодирование речи.
В отличие от скалярного векторное квантование предполагает квантование набора параметров, как единого вектора, впервые использовалось в 50-х годах, но широкое применение началось после того как для кодирования речи стало применяться линейное предсказание.
Анализ-синтез речи с использование векторного квантования.
передатчик
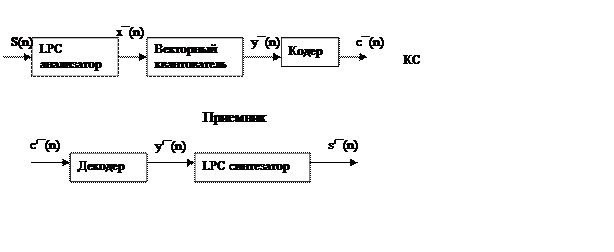
Анализатор на основе LPC фильтра выделяет вектор не квантованных параметров x¯(n) набор параметров квантуется и преобразуется в вектор y¯(n), который далее кодируется в виде последовательности бит c¯(n), на приемной стороне выполняется обратная последовательность операций, однако точное восстановление невозможно, как из за ошибок при передаче, так и вследствие того что восстановление речевого сигнала на приемной стороне производится по квантованным значениям вектора коэффициентов.
Постановка задачи.
Пусть x¯=(x1,x2,x3….xn), n-мерный вектор компоненты которого действительные, случайные величины с непрерывным распределением амплитуд значений. При векторном квантовании n-мерный вектор x¯ отображается в n-мерный вектор y¯ с дискретными значениями амплитуд.
y¯=q(x¯)
Обычно вектор y¯принимает одно значение из ограниченного множества Y¯
Y¯=(yi, i от 1 до L )
Множество Y¯ называют кодовой книгой преобразования, а L размером кодовой книги при этом само значение yi¯ называют кодовым вектором или эталоном.
Для построения кодовой книги n-мерное пространство случайных векторов x разделяется на L областей (или ячеек), которые обозначим как, Ci, (i от 1 до L) каждой ячейкой Ci связывается один единственный вектор yi¯ , при этом квантователь назначает вектору x вектор yi¯ если x¯Є Ci
yi¯=q(xi¯) x¯Є Ci
При векторном квантовании возникает ошибка квантования которая может быть оценена мерой отклонения d(x¯,y¯).
Пример.
Пусть вектор x¯=(x1,x2), L=16
в этом случае:
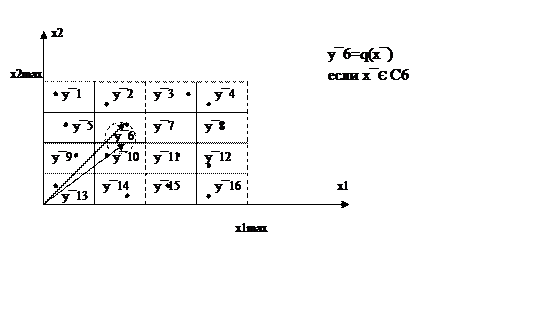
В рассмотренном случае вместо вектора параметров x принимающих неквантованные значения передается вектор y¯6, а точнее номер ячейки 6 вектора y6 в кодовой книге на приемной стороне.
Построение кодовой книги.
Векторный квантователь называют оптимальным, если мера отклонения d(x¯,y¯) минимизирована по всем x и y, для кодовой книги заданной размерности L. Существуют два необходимых условия оптимальности. Первое условие заключается в том, что в оптимальном квантователе должно быть использовано правило выбора по минимуму искажения вектора x т.е. практически производится выбор ближайшей ячейки, а именно: yi¯=q(x¯), тогда и только тогда
d(x¯,yi¯)=< d(x¯,yj¯) j от 1 до L (i=j).
Второе условие оптимальности состоит в том, что каждый кодовый вектор yi¯ должен выбираться из условия минимизации среднего искажения в ячейке Ci, то есть минимизируется следующее расстояние:
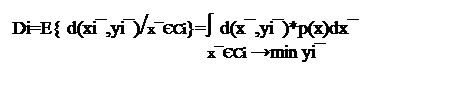
При этом некоторый вектор yi¯* минимизирующий указ. расстояния называют центройдом ячейки Ci и записывают:
yi¯*=centr(Ci)
Для построения кодовой книги на практике задаются набором обучающих векторов x¯(n), n от 1 до M и L-мерным множеством ячеек кодовой книги.
Все векторы x¯(n) распределяются по отдельным ячейкам
Ci, i от 1 до L, при этом если заданы значения центройдов yi¯*, i от 1 до L,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.