Математическая постановка задачи оптимального проектирования цифровых фильтров. Основные типы фильтров частотной селекции и их применение, страница 15

Должны быть известны корреляционная матрица входного сигнала R и вектор взаимной корреляции P.

Определение оптимального значения вектора коэффициентов связано с необходимостью обращения матрицы R, что при большой размерности вектора коэффициентов N весьма проблематично.

Рассмотрим альтернативный подход, связанный с реализацией градиентных методов поиска экстремума рабочей функции .

Прежде всего отметим, что поскольку рабочая функция является квадратичной, достигающей минимального значения при H=Hopt, то можно ввести следующее представление рабочей функции:

                                                                     (5.7)

Раскрываем произведение векторов и матриц выражения (5.7) и с учетом (5.6) можно показать, что (5.7) сводится к (5.3), т.е. к исходному уравнению для рабочей ф-ции.

2.20. Адаптивные фильтры. Классификация и применение.

Цифровой фильтр с переменными параметрами преобразующий пространство входных сигналов X(n)  в пространство выходных сигналов У(n)  с целью воспроизведения желаемой функции передачи назовем адаптивным или фильтром с саморегулированием, если при изменении модели пространства сигналов или цели преобразования он обладает свойствами саморегулирования по заданному критерию качества

z- это цель преобразования

hk(n)- переменные коэффициенты фильтра

Адаптивные фильтры разделяют на два больших класса:

1)  Фильтры без ОС ( без предварительного обучения)

2)  Фильтры с ОС ( с предварительным обучением)

Фильтры без ОС

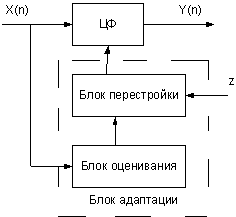
Процесс адаптации без ОС состоит в измерении ( оценивании) характеристик входного сигнала x(n) и в перестройке параметров ЦФ при изменении.

Возможно так же перестройка при смене целей преобразования z.

Процесс адаптации без ОС предполагает что существует и заданы аналитические( алгоритмические) методы синтеза структуры и параметров оператора преобразования F, которые обеспечивают достижение поставленной цели преобразования. Например реализация оптимального Винеровского фильтра по известным корреляционным свойствам сигнала и помехи.

Фильтры с ОС ( с предварительным обучением)

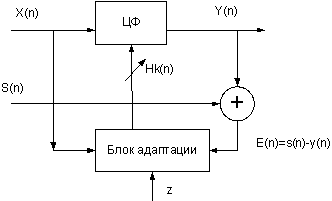
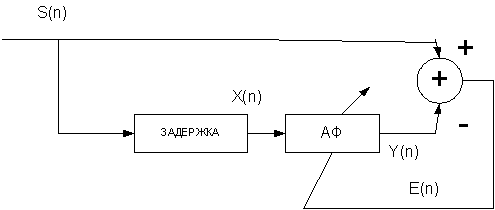
s(n)- обучающий сигнал

Е(n)- ошибка обучения

Процесс обучения предполагающий наличие обучающего сигнала состоит в том, чтобы минимизировать ошибку обучения.

Достоинством алгоритма адаптации с ОС является их работоспособность во многих приложениях там где алгоритмы без ОС не работают.

Например когда не существует эффективных аналитических или алгоритмических методов синтеза желаемого оператора преобразования F.

В случае когда система является нелинейной с изменяющимися параметрами.

Недостатки метода:

1)  Процесс адаптации с ОС может быть неустойчивым

2)  Оптимизация не всегда приводит к глобальному решению в следствии многоэкстремальности рабочей функции

Применение адаптивных фильтров с ОС

1)  Идентификация динамической системы( прямое моделирование)

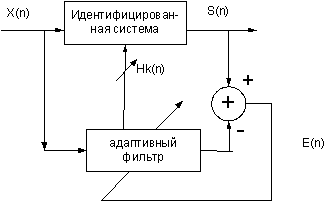
Обучающим сигналом является выходной сигнал идентифицированной системы в процессе адаптации адаптивный фильтр стремится воспроизвести передаточную функцию идентифицируемой системы.

2)  Выравнивание характеристик динамической системы ( обратное моделрование)

                

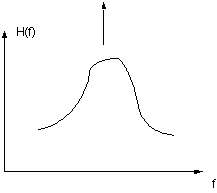
H(f)* H*(f)=1- в диапазоне рабочих частот

В качестве обучающего сигнала используется входной сигнал выравниваемой системы, при этом АФ считается настроенным если его выходной сигнал y(n) совпадает с входным сигналом системы задерженным на время его задержки при прохождении через выравниваемую систему и АФ.

3)Устройство предсказания

X(n)=s(n-k)

Предполагают что АФ в процессе адаптации предсказывает значение входного сигнала x(n) на к-периодов дискретизации. Для фильтра с линейным предсказанием к=1

Данная схема находит широкое применение в устройствах сжатия речи звука и изображения, которые основываются на том , что в канал связи передается вместо сегмента реального сигнала параметры фильтра с линейным предсказанием и ошибка предсказания.

3)  Компенсатор помех

S*(n)=S(n)+p(n)

x(n)=p*(n)