Математическая постановка задачи оптимального проектирования цифровых фильтров. Основные типы фильтров частотной селекции и их применение, страница 6

  Проявляет себя с тех случаях, когда реализуется несколько фильтров одного и того же порядка, но имеющими разные желаемые функции передачи. При этом для всех фильтров используют один и тот же элементарный гребенчатый фильтр и одно и тоже множество цифровых резонаторов.

Наибольший практический интерес при синтезе цифровых фильтров частотной селекции представляет метод двойного  отображения на основе алгоритма БПФ. В основе данного метода лежит фундаментальное свойство ДПФ, которое заключается в том, что произведение Фурье образов входной последовательности и коэффициентов фильтра в точности соответствует Фурье образу выходной последовательности.

Используя алгоритм БПФ для выполнения прямого и обратного ДПФ и алгоритм секционирования для перехода от круговой свертки к линейной, удается достичь наименьших вычислительных затрат и возможности реализации высокоизбирательных фильтров, работающих в широком диапазоне частот.

Стремление уменьшить объем вычислительных затрат за счет исключения  из общего алгоритма обработки наиболее трудоемких в вычислительном отношении операций – операций умножения привело к разработке и применению алгоритмов БПУ и ТПЧ. Однако в связи с ориентацией схемотехнических решений в области ЦОС на применение процессоров обработки сигналов, для которых операция умножения соизмерим по времени выполнения с остальными операциями, перспектива практического использования таких подходов значительно сузила свои границы и представляет интерес только для разработчиков программного обеспечения универсальных микропроцессорных систем.

2.7. Методы построения структур ЦФ в классе БИХ-цепей.

Пусть передаточная функция в классе БИХ цепей задана выражением вида:

(*)

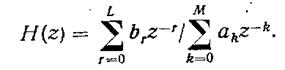
Она однозначно определяет форму оператора F линейного преобразования сигналов:

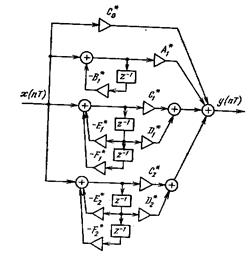
Используя введенные ранее графические изображения для элементарных цифровых звеньев, прямую форму  структуры БИХ цепи представим в виде:

Заметим, что верхняя половина структуры формирует нули, а нижняя полюса. Меняя порядок формирования нулей и полюсов получим новую форму прямой реализации.

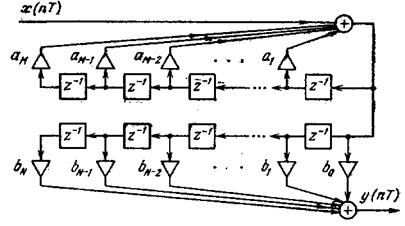
В данной структуре одна ЛЗ избыточна. Сохранив ЛЗ длинной М (М>=L) перейдем к канонической структуре :

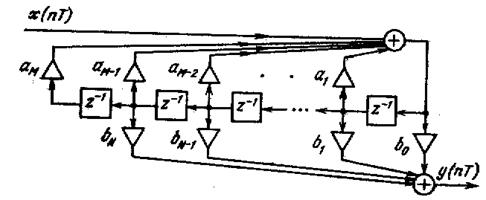
Каноническая структура отличается минимальным объемом памяти.

В силу зависимости устойчивости БИХ фильтров от порядка М на практике в рамках канонической формы реализуют фильтры не выше 5 порядка, а чаще не выше 2-го.

На практике широкое применение нашли каскадная и параллельная форма  реализации структуры БИХ звеньев 1-го и 2-го порядков.

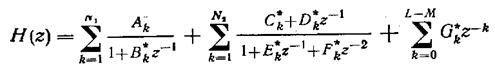Переход от прямой формы к параллельной выполняется путем разложения  дробно-рациональной функции на простые дроби, при этом передаточная функция примет вид:

 - число звеньев 1-го и 2-го порядка соответственно.

Если числитель и знаменатель в (*) разложить на простые множители, то получим:

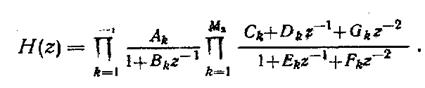
Выводы:

Переход от прямой формы построения к параллельной и каскадной предоставляет разработчику ряд существенных преимуществ:

1. Значительно уменьшается чувствительность характеристик цифровой цепи к неточному представлению коэффициентов.
2. Появляется свобода в выборе коэффициентов и способе распределения отдельных блоков с позиции минимизации уровня собственных шумов.
3. Открывается возможность простой многопроцессорной реализации ЦФ, работающего в режиме реального времени на высокой частоте дискретизации.

2.9. Дискретное преобразование Фурье и алгоритм БПФ.

Пусть последовательность , задана на конечном интервале длительностью  и может быть периодически продолжена с периодом, равным . Тогда имеет место пара дискретных -точечных преобразований вида

 

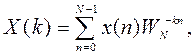(1)

 

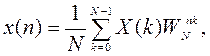(2)

 

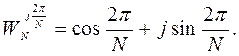где

Прямое ДПФ (1) определяет по заданной временной последовательности  -мерный массив коэффициентов Фурье , а обратное ДПФ (2) позволяет восстановить исходную временную последовательность  по заданному массиву коэффициентов Фурье.