Проблема анализа влияния собственных шумов и неточного представления параметров оператора Р на точность воспроизведения желаемых характеристик.
Проблема синтеза малошумящих и низкочувствительных к неточному представлению параметров структур оператора Р. В зависимости от формы построения цифровой цепи и выбора ее параметров, влияние собственных шумов и неточного представления коэффициентов на конкретный результат обработки может быть различным, поэтому важной проблемой синтеза структуры оператора Р, является проблема построения малошумящих и низкочувствительных структур цифровой цепи.
Проблема выбора схемотехнического решения:
Классы ЦСП;
Семейство процессорных модулей;
Создание эффективного программного обеспечения.
Проектирование цифровых фильтров частотной селекции с точки зрения современных представлений теорий цифровых цепей включает в себя три основных этапа:
1) выбор класса цифровых цепей и аппроксимация желаемых частотных характеристик фильтра в пространстве функций, строго воспроизводимых заданным классом цифровых цепей;
2) выбор метода проектирования или поиск структуры цифре вой цепи, отличающейся возможностью эффективной программной или аппаратной реализации;
3) реализация цифрового фильтра.

Исходную линейную цифровую цепь представим как совокупность элементарных цифровых звеньев, соединенных друг с другом определенным образом. К числу элементарных цифровых звеньев отнесем сумматор, умножитель на константу и элемент задержки на один период дискретизации Т. Правило, по которому эта цепь отображает воздействие х(пТ) в реакцию у(пТ), обозначим F и назовем оператором цифровой цепи.
Под проектированием линейной цифровой
цепи в самом общем случае будем понимать синтез некоторого оператора F, выполняющего линейное преобразование пространства сигналов
х(пТ) с целью воспроизведения заданной функции передачи ![]() , где
, где ![]() - приведенная
круговая частота, измеряемая в радианах и принимающая непрерывные значения в
диапазоне
- приведенная
круговая частота, измеряемая в радианах и принимающая непрерывные значения в
диапазоне ![]() . В зависимости от принятой
структуры линейной цифровой цепи, которая, в свою очередь, зависит от
используемого метода проектирования, оператор F имеет различное математическое содержание. Поэтому будем
полагать, что различным структурным реализациям оператора F соответствуют различные подклассы
. В зависимости от принятой
структуры линейной цифровой цепи, которая, в свою очередь, зависит от
используемого метода проектирования, оператор F имеет различное математическое содержание. Поэтому будем
полагать, что различным структурным реализациям оператора F соответствуют различные подклассы ![]() класса
операторов
класса
операторов ![]() , обеспечивающих
воспроизведение с наперед заданной точностью желаемой функции передачи
цифровой цепи
, обеспечивающих
воспроизведение с наперед заданной точностью желаемой функции передачи
цифровой цепи![]() , представляющей в данном случае
комплексную частотную характеристику цепи.
, представляющей в данном случае
комплексную частотную характеристику цепи.
Пространство
функций передачи цифровой цепи, строго воспроизводимых в классе операторов GF, обозначим R. При этом
желаемая функция передачи ![]() может в общем случае и
не
принадлежать пространству R. Однако для
произвольной
может в общем случае и
не
принадлежать пространству R. Однако для
произвольной ![]() должна существовать такая последовательность воспроизводимых в каждом из
подклассов
должна существовать такая последовательность воспроизводимых в каждом из
подклассов ![]() функций передачи
функций передачи ![]() ,
при которой для любого сколь угодно малого
,
при которой для любого сколь угодно малого ![]() >0
можно было найти такое n, при котором для всех l>=п имело бы место неравенство
>0
можно было найти такое n, при котором для всех l>=п имело бы место неравенство ![]() , где
, где![]() —метрика пространства
функций R. Иначе говоря, в
пространстве R строго
воспроизводимых функций передачи должна существовать сходящаяся последовательность,
пределом которой является желаемая функция
передачи. .
—метрика пространства
функций R. Иначе говоря, в
пространстве R строго
воспроизводимых функций передачи должна существовать сходящаяся последовательность,
пределом которой является желаемая функция
передачи. .
Используя введенные выше
понятия и обозначения, задачу проектирования линейно цифровой цепи сформулируем
следующим образом: найти подкласс ![]() класса операторов GF и оператор F
класса операторов GF и оператор F![]() , такие, что:
, такие, что:
![]()
где ![]() — допустимое отклонение
в метрике пространства R.
— допустимое отклонение
в метрике пространства R.
Если цель
проектирования связана не только с воспроизведением заданной функции передачи,
но и с оптимизацией некоторогокритерия качества (целевой функции) ![]() при одновременном выполнении граничных
условий
при одновременном выполнении граничных
условий ![]() ,то задача оптимального проектирования
формулируется в виде: найти подкласс
,то задача оптимального проектирования
формулируется в виде: найти подкласс ![]() класса операторов GF и оператор F
класса операторов GF и оператор F![]() , такие, что:
, такие, что:
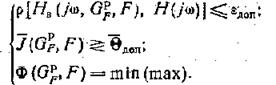
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.