Получение навыков количественных оценок эффектов и явлений в структуре полупроводников и интегральных микросхем, страница 8

Полагается, что размеры кристалла в общем случае не ограничены.

Напрашивается вывод, что нужно учитывать периодичность полей в кристаллической структуре, для чего нужно отказаться от представления кристалла как потенциального ящика и рассмотреть некоторое приближение к реальности. Самым очевидным приближением является учёт периодичности потенциальной энергии в структуре. То есть можно представить потенциальную энергию как функцию от координаты в пределах одной ячейки, периодически повторяющейся при переходе к соседней ячейке:

, где n_i – некоторое целое число;

c_i – постоянная решётки в соответствующем направлении.

Это означает, что во всех ячейках, образующих структуру твёрдого тела закономерность изменения потенциальной энергии по координате сохраняется.

Выполнение этих условий означает, что для определения свойств электронной системы в кристаллической структуре достаточно исследовать события в масштабах одной ячейки. Таким образом вместо решения уравнения Шредингера для каждого электрона можно перейти к одноэлектронному приближению.

Решение уравнения Шредингера для этого случая имеет вид:

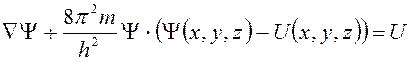уравнение для трёхмерной ячейки.

Волновая функция трёхмерного кристалла может быть представлена как произведение волновых функций, найденных для каждой координаты:

.

Ранее кристалл рассматривался как один потенциальный ящик. Теперь мы представляем кристаллы в виде периодической структуры чередующихся потенциальных ям.

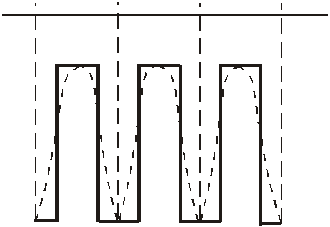Этот рисунок показывает распространение силовых потенциальных полей.

Первым приближением, позволяющим учесть периодическую структуру, является замена видов распространения некими потенциальными ящиками.

Потенциальная яма отождествляется с узлом, барьер – с междоузлием. Для того, чтобы определить значения волновых функций, необходимо решить уравнение Шредингера с учётом существования потенциальных барьеров и их конкретных характеристик: высоты, ширины, то есть вместо решения уравнения Шредингера для ящика ищем решение для двух ящиков, разделённых потенциальным барьером.

a – ширина основания потенциальной ямы;

c – постоянная решётки;

b – ширина барьера;

U₀ – высота барьера.

Если мы хотим найти характеристики волновой функции, определяющей вероятное нахождение частицы в любой области, то мы должны искать решение уравнения Шредингера в виде, применимом для областей 1,2,3.

Совместное решение для областей 1,2,3:

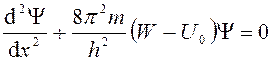
Для  второй области:

.

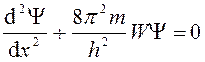Найдём решение в экспоненциальной форме для случая, когда b ® 0,       U₀ ® ¥, так что bU₀ = const:

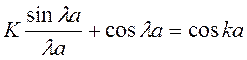, то есть частица в этой системе может находиться только тогда, когда выполняется данное равенство. Если оно не выполняется, то это значит частицы не существует.

Лекция № 9

Исследование решения уравнения Шредингера для периодической структуры

Если электрон может находиться в системе периодических потенциальных барьеров, то его энергетические характеристики должны отвечать уравнению:

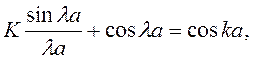                                         (1)                   

где k – волновой вектор;

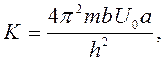
где а – ширина основания потенциального ящика,

b – ширина барьера, U₀ – высота барьера, m – масса частицы.

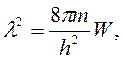                                                               (2)                                         

где W – кинетическая энергия.

Это уравнение трансцендентно, поэтому его корни ищутся графическим методом.

Пусть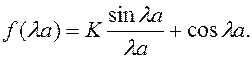

Если > 1, то решений уравнения нет.

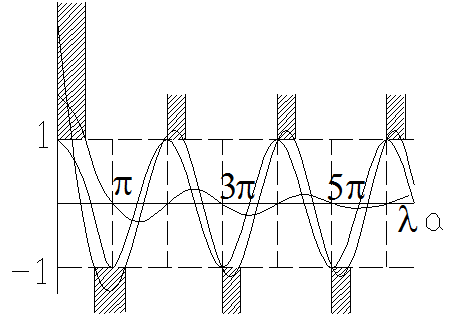Таким образом, графическая интерпретация показывает, существуют значения аргумента , при которых уравнение не имеет решений, то есть нет соответствующих значений энергии микрочастиц. Заштрихованная область соответствует запрещенным значениям энергии частиц в периодическом поле. Ширина таких запрещенных зон по мере увеличения значения аргумента  - уменьшается, то есть ширина разрешенных зон возрастает.