Получение навыков количественных оценок эффектов и явлений в структуре полупроводников и интегральных микросхем, страница 2

d - начальная фаза,

а – амплитуда,

w = 2pu - круговая частота.

Пусть наблюдатель находится на расстоянии r от источника.  - радиус-вектор. Так как волна распространяется со скоростью света (конечной скоросью), то

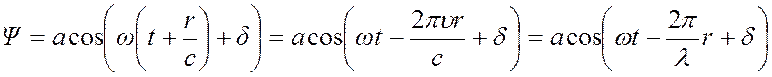
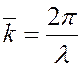 - волновой вектор. В теории колебаний все характеристики колебательных процессов выражены через .

.

Такой колебательный процесс называется плоской монохроматической волной.

Комплексное представление колебательного процесса основывается на формуле Эйлера:

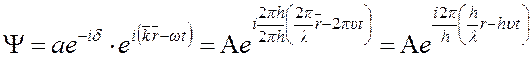
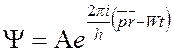 - выражение волны де Бройля.

Лекция №3

Волны де Бройля

Экспоненциальная форма записи плоской монохроматической волны:

.

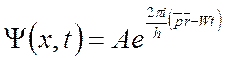Выделим временную часть:

.

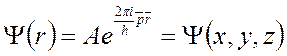Используя формулу Эйлера, запишем:

.

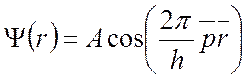Если эта функция имеет тригонометрическую форму и выражается в виде тригонометрической функции, это значит, что она имеет положительные и отрицательные значения. Смысл исследования волнового движения частиц заключается в том, чтобы определить координаты этой частицы. С этой целью де Бройлем было предложено волновое описание распределения частиц в пространстве:

.

В такой форме предлагалось представлять некоторую плоскую монохроматическую волну. Если раскрыть аргументы в показатели степени, мы получим то же выражение, что и для монохроматической волны (разница только в знаке).

Волновое представление необходимо для определения положения частицы в пространстве, для этого используется часть выражения, зависящая только от координаты, потому что другая часть (зависящая от времени) является энергетической характеристикой. Используют характеристику, которая называется «квадрат модуля волновой функции», то есть рассматривают .

Определение: физический смысл функции  заключается в том, что квадрат модуля этой величины является вероятностью нахождения частицы в некоторой точке пространства с координатой х в момент времени t.

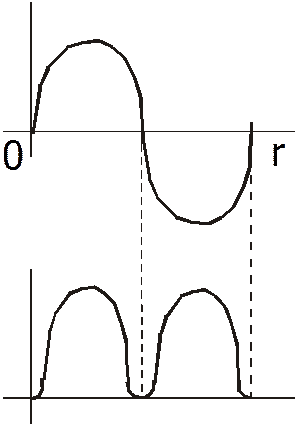Если квадрат модуля достигает максимума в некоторой точке пространства, это означает, что вероятность нахождения частицы здесь максимальна. В отличие от волновых процессов в свободном пространстве здесь предметом изучения является, например, электрон в твёрдом теле. При этом полагается, что твёрдое тело имеет ограниченный объём. Эти ограничения существенно влияют на характеристики волновой функции. Если размеры твёрдого тела неограниченны, то характеристики микрочастицы могут быть теми же самыми, что и в свободном пространстве с некоторыми уточнениями (энергия должна быть квантована). При стягивании размеров в точку появляются дополнительные ограничения на возможные значения энергии частиц. Появляются области разрешённых (запрещённых) значений энергии. В пределах разрешённой области энергия дополнительно дискретизуется.

Волновое представление движущихся микрочастиц, обладающих кинетической энергией, позволило в конечном итоге установить квантовую природу возможных значений энергии микрочастиц и установить взаимосвязь между квантованными значениями энергии с размерами области локализации микрочастиц. В теоретической физике это связывают с понятием потенциальной ямы.

Уравнение Шредингера

Формально плоская монохроматическая волна де Бройля является результатом решения уравнения Шредингера, что даёт возможность получить вероятностную оценку положения микрочастицы в пространстве.

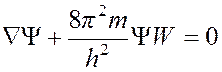 - формальная запись уравнения Шредингера,  где

W – кинетическая энергия частицы.

Для случая одномерного представления волнового процесса (анализ событий в потенциальной яме), уравнение Шредингера имеет вид:

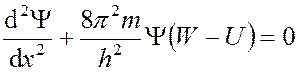, где W – полная энергия частицы,

U – потенциальная энергия.

Кинетическая энергия классической частицы:

;

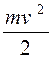кинетическая энергия частицы твёрдого тела, обладающей волновыми свойствами:

.

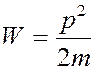Возникает вопрос: при волновом описании движения частицы каким образом с помощью волнового процесса определить пространственное положение микрочастицы?