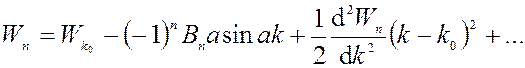Получение навыков количественных оценок эффектов и явлений в структуре полупроводников и интегральных микросхем, страница 15

, где - граница зоны.

На границах зоны два слагаемых ряда обращаются в ноль, но так как интерес представляют граничные электроны, то для них запишем:

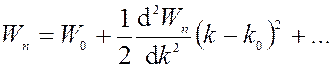, где n – номер дискретного уровня, примыкающего к границе.

Для электронов, находящихся в потенциальном ящике можно записать:

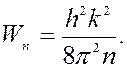
При смещении основания потенциального ящика не на нулевой уровень потенциальной энергии:

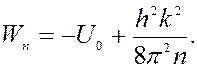
Приравняем полученные значения энергий:

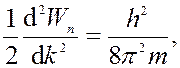
следовательно,

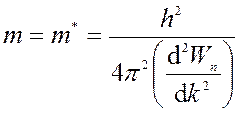, где  - эффективная масса.

Для граничных электронов введение понятия эффективной массы открывает возможности применения к этим электронам законов классической механики, и тем самым избавляет от необходимости использования квантовых представлений для решения ряда прикладных задач. Это означает, что законы движения электронов, находящихся на границах зоны в периодической структуре силовых полей, подчиняются классическим законам, но отличие эффективной массы от массы электрона позволяет учесть влияние периодической структуры на движение таких носителей. Это позволяет раскрыть закономерности перестройки электронной системы при сообщении ей энергии извне. Можно рассмотреть две различные ситуации: применительно к полупроводникам граничные электроны появляются, когда электрон переходит из валентной зоны в зону проводимости, следовательно, можно определить эффективную массу электронов в зоне проводимости.

Поскольку любой уровень зоны проводимости расположен выше граничного уровня, то есть  то эффективная масса приграничных электронов зоны проводимости является величиной положительной. Если эти электроны образовались в результате перехода из валентной зоны, оставив там дырки, то для валентной зоны разность между граничным уровнем и любым приграничным всегда меньше нуля. Использование этой модели позволяет объяснить различия в знаках эффективных масс электронов и дырок. Отрицательный знак эффективной массы дырки означает, что импульс тоже становится отрицательным. Если знак отрицательный, то под действием силы движение частицы происходит в направлении противоположном вектору действия этой силы.

Ширина зон разрешённых значений энергии по мере увеличения номера зоны возрастает. Это означает, что расстояние между энергетическими уровнями в различных зонах различно. В частности, расстояние между соседними уровнями в зоне проводимости меньше расстояние между уровнями в валентной зоне.

 ~ , то есть эффективная масса обратно пропорциональна расстоянию между соседними уровнями. Это означает, что эффективная масса электронов в зоне проводимости будет меньше, чем эффективная масса дырок на приграничных уровнях валентной зоны. Это позволяет оценивать различия полупроводниковых структур, где в качестве основных носителей используются электроны и дырки. Подвижность дырок всегда меньше подвижности электронов, поэтому микроструктуры, где в качестве основных носителей выступают дырки, имеют худшие динамические характеристики по сравнению с электронами.

Для правильного истолкования и количественных оценок всех эффектах в полупроводниках необходимо использовать в расчётных соотношениях эффективные массы.

Статистика электронов в полупроводниках

Основной задачей физики твёрдого тела применительно к полупроводникам является определение числа электронов и дырок в зоне проводимости и валентной зоне беспримесных и примесных полупроводников.

Формальная постановка такой задачи известна. Пусть N₁ – число электронов в зоне проводимости беспримесного полупроводника, тогда

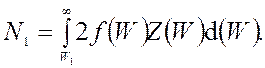
Лекция №15

Статистика электронов в полупроводников.

Постановка основной задачи в полупроводниках

В полупроводниках основная задача предусматривает определение количества носителей заряда в разрешенных зонах и способа их распределения по энергетическим уровням. Для решения этой задачи привлекается квантовая статистика Ферми-Дирака (применительно к невырожденным полупроводникам), то есть уровень Ферми находится в запрещенной зоне ниже нижней границы зоны проводимости и выше верхней границы валентной зоны. Во всех случаях число электронов и дырок считается малым, что является следствием отсутствия вырождения. Но применительно к полупроводникам есть некоторые особенности. Например,