Важнейшим выводом, вытекающим из теории Зоммерфельда, является установление квантовой природы носителей заряда, а именно: квантование энергии и импульса. То есть нельзя с позиций классических представлений определить характеристики электрона в определенном объеме локализации. Была установлена взаимосвязь волновой функции с энергией, вероятностные характеристики координат частиц. Но теория Зоммерфельда не дает ответа на главный вопрос: как распределяются по энергиям электроны в составе некоторой системы.
Для решения основной задачи необходимо знать закон распределения электронов по состояниям. Такая задача решается в рамках статистики Ферми-Дирака. Исходя из статистической теории, был разработан закон равновесной вероятности распределения электронов по состояниям.
Второй закон термодинамики для равновесного распределения является с одной стороны наиболее вероятным, с другой стороны, система может находиться в нем неограниченно большое время, с третьей стороны, система обладает в таком состоянии минимальной внутренней энергией. В основе положений теории Ферми-Дирака лежит следующее:
1.одинаковые частицы (электроны в твердом теле) неразличимы, обмен состояниями между двумя любыми парами частиц не изменяет системы в целом;
2. электроны подчиняются принципу Паули: в одном состоянии могут находиться не более двух электронов с противоположными спинами;
3. число состояний в конечном интервале ![]() конечно.
конечно.
Пусть в некотором интервале энергии ![]() имеется некоторое число состояний dZ и некоторое число электронов N.
Тогда вероятность нахождения я электрона в этом интервале:
имеется некоторое число состояний dZ и некоторое число электронов N.
Тогда вероятность нахождения я электрона в этом интервале:
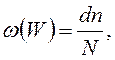
где dn – число фактически находящихся в этом интервале электронов.
Функция распределения электронов по состояниям –
вероятность заполнения одного состояния в интервале энергии ![]() :
:
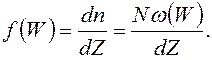
До этого мы рассматривали ситуацию в
многоэлектронном истолковании, теперь же переходим к одноэлектронному
приближению. Если известна величина ![]() , то мы можем определить
для любой системы вероятность заполнения всех существующих состояний, а при
известном числе состояний ещё и общее число электронов.
, то мы можем определить
для любой системы вероятность заполнения всех существующих состояний, а при
известном числе состояний ещё и общее число электронов.
Исходя из общих законов статистики, функция распределения была определена:
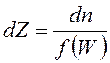 ,
,
![]()
Введение функций распределения ![]() создает предпосылки для решения основной
задачи, используя определение функции плотности распределения и функции
распределения по состояниям. Проблема сводится к определению вида функции
создает предпосылки для решения основной
задачи, используя определение функции плотности распределения и функции
распределения по состояниям. Проблема сводится к определению вида функции ![]() . Применительно к
квантовым системам Ферми и Дираком эта функция была найдена:
. Применительно к
квантовым системам Ферми и Дираком эта функция была найдена:
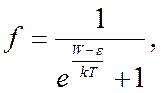
где W – значение энергии, вблизи которого мы рассматриваем приращения, kT - энергия теплового движения электрона, ε – некоторое значение энергии, при котором вероятность заполнения составляет 50% - уровень электрохимического потенциала – уровень Ферми. Положения уровня Ферми определяет свойства электронной системы. Рассмотрим случаи:
1. нулевых температур и малых энергий;
2. малых, но отличных от нуля температур.
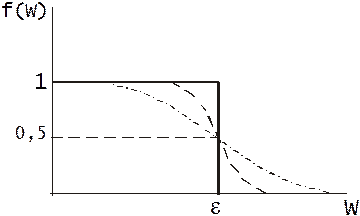 |
Деформация (сглаживание) функции по мере возрастания температур означает, что возрастает вероятность заполнения состояний на уровнях, расположенных выше уровня Ферми. То есть появляются состояния на энергетических уровнях выше уровня Ферми с небольшой, но отличной от нуля вероятностью заполнения. Плотная упаковка сферы в пространстве импульсов разрыхляется в поверхностном слое, и за пределами этой сферы появляются новые состояния. При дальнейшем увеличении температуры вырождение отсутствует.
В металлах электронная система вырождена при комнатной температуре, то есть 98% электронов металла находятся на уровнях, отстоящих от уровня Ферми на величину kT. То есть для металлов функция распределения имеет тот же самый вид, как и при Т = 00 . В полупроводниках же система является невырожденной, распределение происходит так же, как в классической системе.
Лекция № 7
Состояние электронов в металлах
Функция распределения Ферми-Дирака:
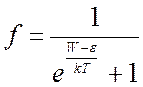 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.