Получение навыков количественных оценок эффектов и явлений в структуре полупроводников и интегральных микросхем, страница 7

Разнообразие вариантов соотношений между величинами W и ε соответствует реальным ситуациям, определяет степень вырождения системы и в конечном итоге принадлежность системы  -  классической или квантовой.

Если dn – функция распределения на dz, то

 - общая постановка основной  квантово-механической задачи.

Для того, чтобы подойти к решению этой задачи используют различные приближения, так как в общем виде она не решается. Рассмотрим случай нулевой температуры (полезен для анализа невырожденных систем). Пусть         Т = 0,  тогда

W > ε, ,  значит,

  , значит,

Тогда вычисление числа электронов, находящихся в  интервале от 0 до ε:

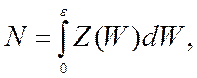
то есть число электронов в данном интервале энергий равно числу состояний, значит, все возможные состояния заняты.

.

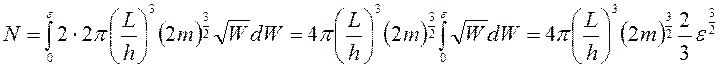Решим уравнение относительно ε:

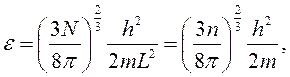
где 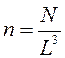 - концентрация электронов.

Имея в виду, что эта система – металл, в котором все уровни заполнены и верхним является уровень ε. В реальных металлах ε принимает  значения порядка 8 – 9эВ.

Можно ожидать, что  средняя и полная энергии при 0⁰ К будут отличны от нуля, что нге может быть достигнуто в классических системах.

Для определения средней энергии электрона воспользуемся выражением:

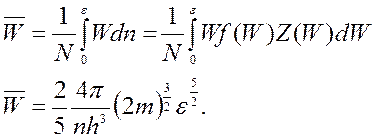
Если подставить теперь ε в выражение для средней энергии, то получим:

.

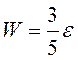Тогда полная энергия системы:

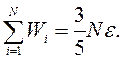
То есть установлена связь между уровнем Ферми и  средним значением энергии электрона. При комнатной температуре такие оценки сохраняются и для металлов, значит, можно определить значения энергии системы. Пусть средняя энергия составляет 5эВ, тогда в 1см³ заложена энергия 5*10²⁴эВ.

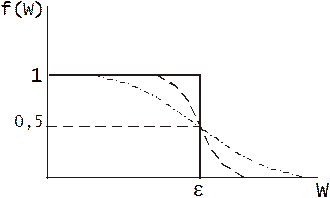
Графическая интерпретация функции распределения Ферми-Дирака:

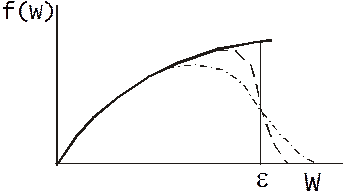При абсолютном нуле в вырожденной системе в пространстве импульсов все состояния умещаются в объёме сферы радиусом  в которой все места (ячейки) заняты. По мере увеличения температуры, когда , самые плотные слои сферы начинают разрушаться, верхние же слои частично освобождаются. Для металлов характерен выход 2 –3% электронов за пределы сферы.

Критерии (факторы) вырождения электронной системы

Пусть выполняется условие:

1.  - критерий вырождения системы. Если ε намного больше некоторого уровня, который сам по себе мал, и поэтому может быть соотнесен с условным нулем, значит, уровень Ферми размещается значительно выше наинизшего уровня в данной системе. Это означает, что все энергетические уровни в данной системе и соответствующие им состояния заполнены.

2. , то есть уровень, принятый за  нулевой, находится ниже уровня Ферми, значит, , и функция Ферми будет стремиться к нулю.

В самом общем случае признаком отсутствия вырождения является возможность пренебречь единицей в знаменателе и представить функцию Ферми-Дирака в виде:

.

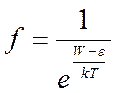Значит, для невырожденных систем можно записать:

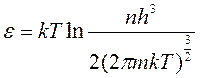
Лекция №8

Если , то система является невырожденной, это означает, что наличие или отсутствие вырождения определяется положением уровня Ферми. Если этот уровень устремляется вниз, то система стремится к снижению степени вырождения, и наоборот. Если система не вырождена, то к ней применима квантовая статистика, если нет, то можно использовать классическую статистику. Из выражения для энергии уровня Ферми вытекает:

-

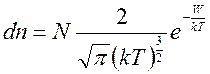
-  это классическое соотношение, называемое распределением Максвелла-Больцмана. Оно применимо для невырожденных систем. Из него вытекает условие вырождения:

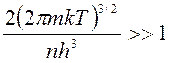
Если система состоит из неких частиц с большой массой и малой концентрацией, то условие выполняется.

Если концентрация увеличивается, то система близка к вырождению.

Состояние электронов в периодическом силовом поле

Достоинства теории Зоммерфельда заключаются в том, что она позволила определить следующее:

1.  дискретное значение энергии микрочастицы, локализованной в некотором объёме;

2.  теоретически определила количественную меру возможных дискретных значений энергии.