Получение навыков количественных оценок эффектов и явлений в структуре полупроводников и интегральных микросхем, страница 3

При отсутствии ограничений на область распространения волнового процесса утрачивается возможность определения координаты частицы в некоторый момент времени. Возникает противоречие, так как с одной стороны движение частицы – это распространение волны, с другой стороны не удаётся установить связь между местом нахождения частицы и характеристиками волнового процесса. Для определения пространственного положения частицы используют понятие волнового пакета, представляющего собой суперпозицию некоторого множества волн де Бройля, отличающихся одна от другой значениями частоты или значениями волнового вектора. То есть при рассмотрении суммы волн де Бройля с малоотличающимися частотами результат представляется в виде амплитуды колебательного процесса, локализованного в пространстве. Амплитуда такого процесса:

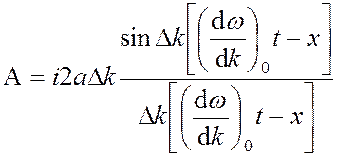, где Dk – предельное отклонение волнового вектора от значения, соответствующего центральной частоте. То есть процесс моделируется функцией вида: 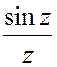. Графически это изображается:

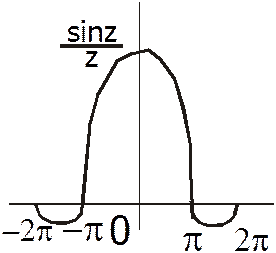Скорость распространения волнового пакета в пространстве называется групповой скоростью и равна скорости движения частицы, отождествляемой с волновым пакетом. Для определения скорости:

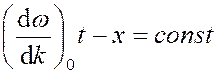, то есть мы отслеживаем волну, двигаясь вместе с ней за точкой фиксированной фазы.

Дифференцируя по времени, получим:

.

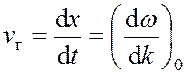Представим эту зависимость иначе:

.

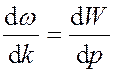Используя волновые представления о движущейся частице, в том числе понятие волнового пакета, мы пришли к выводу, что групповая скорость пакета равна скорости распространения частицы в пространстве.

Лекция №4

Основная квантово-механическая задача

Основная квантово-механическая задача предусматривает определение энергетического спектра электрона в твердом теле. Иными словами, нахождение распределения электронов твердого тела по состояниям и значениям энергии. Решение этой задачи позволяет определить все электрофизические характеристики твердого тела (проводимость, подвижность, время жизни носителей).

Применительно к задачам микроэлектроники решение основной квантово-механической задачи позволяет рассчитать электрические характеристики микроструктур и оптимизировать электрофизические параметры элементов в составе микроструктур. Во всех математических моделях также будут присутствовать решения

Для основной квантово-механической задачи используют различные подходы и упрощения. Первым следует рассматривать попытку решения в теории Зоммерфельда. Основными положениями теории являются: рассмотрение взаимодействия каждого электрона в составе электронного газа с остальными электронами; рассмотрение взаимодействия каждого электрона с периодическими силовыми полями.

Полагается, что результатом всех видов взаимодействий является некое усреднённое постоянное в пределах всего кристалла электрическое поле, независящее от периодичности кристаллической структуры. То есть кристалл твёрдого тела заменяется неким аналогом с постоянным электрическим полем внутри. Потенциал такого поля не зависит от координаты. Если в этом постоянном электрическом поле находится частица, то энергия этой частицы:

, где V – потенциал электрического поля.

По определению потенциалом электрического поля является работа, которую нужно совершить, чтобы переместить единичный положительный заряд из точки с нулевым потенциалом в данную точку поля. Потенциальная энергия определяется потенциалом поля и зарядом частицы. Потенциальная энергия электрона в структуре кристалла в теории Зоммерфельда рассматривается как величина отрицательная, кинетическая энергия частицы рассматривается как положительная величина, следовательно, полная энергия частицы – сумма кинетической и потенциальной энергий:

;

, следовательно,  W < 0, то есть полная энергия является отрицательной величиной.