Получение навыков количественных оценок эффектов и явлений в структуре полупроводников и интегральных микросхем, страница 5

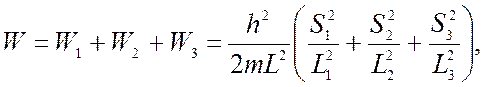
то есть мы рассматриваем кристалл с размерами L₁, L₂, L₃, где L_1,2,3 ≠ ∞.

Если рассматривать кубический кристалл, то

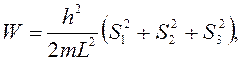
где S₁, S₂, S₃ – квантовые числа.

Каждый конкретный набор квантовых чисел определяет так называемое состояние микрочастицы. Каждое состояние определяет значение энергии. Различные наборы квантовых чисел определяю так называемое вырожденное состояние. То есть в рамках теории Зоммерфельда удалось ввести понятие вырожденных систем. Для вырождения состояний неизменное значение энергии микрочастицы соответствует различной ориентации вектора импульса микрочастицы в трехмерном пространстве. Результирующий импульс электронной системы определяет направление и величину электрического тока: равенство нулю этого импульса (при наличии пар электронов с противоположными импульсами) означает отсутствие электрического тока, отличие от нуля – является признаком существования электрического тока. Введенные в рамках теории Зоммерфельда понятия “состояние”, “вырожденное состояние” позволяют в рамках квантовой теории твердого тела ввести качественные и количественные отличия между свойствами видов твердого тела, в частности  между проводниками, диэлектриками и полупроводниками.

Число возможных состояний электронов в металлах

Число возможных состояний в рамках теории Зоммерфельда в общем случае является неограниченным, но нас интересует число состояний в пределах некоторого интервала. Возьмем интервал dW. Энергия классической частицы:

.

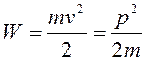Если мы свойства классической частицы (разрешенные значения энергии) сопоставим с разрешенными значениями энергии кантовой частицы, то

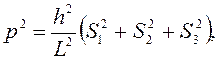
это означает, что импульс состоит из трех компонентов, то есть                    p = p_x +p_y +p_z. Выделим проекции импульса на координатные оси:

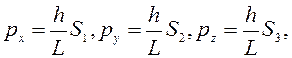
то есть проекции импульса на координатные оси в пространстве квантованы.

Если известно разрешенное значение энергии, то ему соответствует набор квантовых чисел  и набор импульсов по каждой координатной оси. При переходе к трехмерному пространству мы получим некоторую поверхность, перебирая все возможные наборы квантовых чисел. В случае кубического кристалла перебор возможных значений сопровождается различной ориентацией вектора так, что его конец формирует некоторую сферу. При увеличении значения энергии на величину dW, импульс также получит приращениеdp. Для того, чтобы вектор импульса переместить из  одной позиции в другую, на соответствующих координатных осях должно произойти изменение на величину 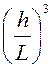, то есть с каждым элементарным объемом 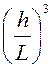 мы соотносим определенное положение импульса в пространстве. С другой стороны, энергии W соответствует импульс p, но во всех случаях конец вектора приходится на точки, принадлежащие сфере. То есть существует некий объем, заключенный между двумя сферами с радиусами p и p+ dp, и задача сводится к определению числа элементарных объемов, которые можно разместить между двумя сферами. Исходя из геометрических представлений, объем, заключенный между двумя сферическими поверхностями:

.

Число состояний в объеме, заключенном между двумя сферическими поверхностями:

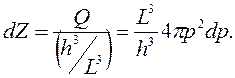
Плотность электронных состояний:

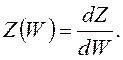
Если p = , тогда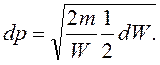

Лекция №6

Определим приращение dZ:

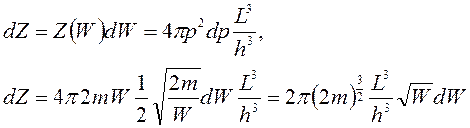
-  число состояний в интервале значений dWсвязано с приращением энергии.

Вывод: приращение числа состояний электронов в металлах в зависимости от энергии происходит по закону корня квадратного. Графическая интерпретация этого закона:

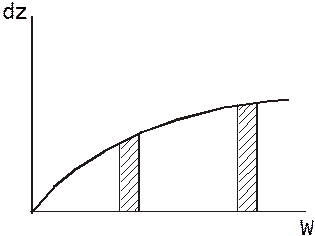Полученные зависимости относятся к числу фундаментальных, используемых для решения основной задачи физики твердого тела – определения числа электронов в заданном энергетическом интервале.

Статистика Ферми-Дирака

Поскольку известное число с известными энергиями позволяет определить электропроводность твердого тела, время жизни носителей заряда, диффузионную длину и т.д., то есть все основные электрофизические характеристики, то без их количественного значения нельзя определить электрические параметры микроприборов, построенных на основе полупроводниковых материалов.