Получение навыков количественных оценок эффектов и явлений в структуре полупроводников и интегральных микросхем, страница 16

где Р – импульс,

W – энергия частицы.

Импульсы граничных электронов равны нулю по определению, следовательно, вносим уточнения:

где  - граничный уровень энергии.

Если мы рассмотрим валентную зону, то граничный уровень располагается выше любого уровня, а в зоне проводимости – ниже любого уровня:

 - выражение для электронов в зоне проводимости;

 - для электронов в валентной зоне.

.

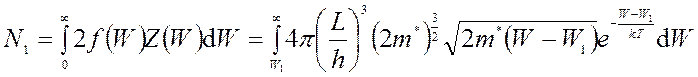В результате получаем:

.

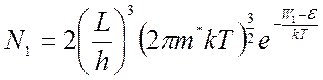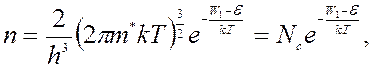
где  - эффективная плотность состояний – предельная плотность электронных состояний в приграничной области зоны проводимости.

.

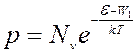Выражения для n и p получены для беспримесного полупроводника.

Графическая интерпретация зависимости энергии от плотности состояний:

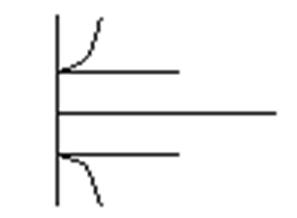
Чем выше энергетический уровень, тем больше состояний приходится на этот уровень.

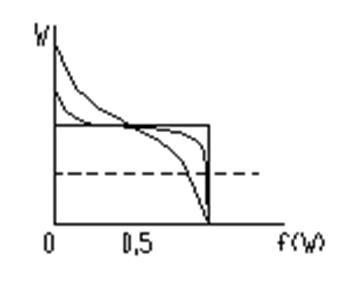
Совместим этот график с графиком функции Ферми-Дирака.

 

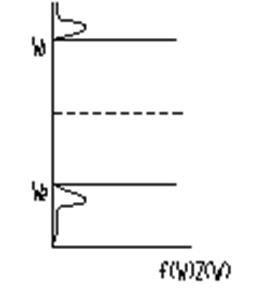
Распределение электронов по энергиям в зоне проводимости и валентной зоне характеризуется зависимостью с четко выраженным экстремумом. То есть существует максимальная плотность распределения электронов по энергиям. График отражает распределение электронов в зоне проводимости и валентной зоне.

Примесный полупроводник

В примесных полупроводниках основным источником электронов являются донорные уровни, а дырок – акцепторные. Его можно рассматривать как беспримесный полупроводник, в котором уровень выполняет роль соответствующей зоны, например, донорный уровень как бы заменяет валентную зону, а акцепторный – зону проводимости.

Пусть имеется донорный полупроводник, для которого на уровне W¢ существуют примесные уровни с плотностью Z¢, в то же время в зоне проводимости имеется N₁ электронов.

Если N₁ = Z¢, то все электроны с этого уровня ушли в зону проводимости; если N₁ < Z¢, следовательно, часть электронов (N¢) осталась на примесном уровне, то есть

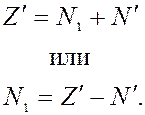
Продолжаем считать, что полупроводник является невырожденным, тогда

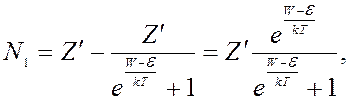
где W находится в зоне проводимости.

В примесных полупроводниках уровень Ферми расположен выше донорного уровня, тогда W¢ - e < 0, следовательно,  много меньше единицы, тогда

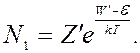
Для беспримесного полупроводника:

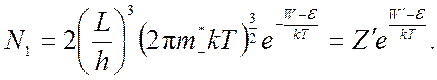
Из этого уравнения можно определить энергию уровня Ферми:

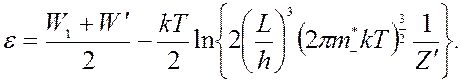
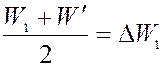 - энергия активации.

Подставляя выражение для e в формулу нахождения, получим:

.

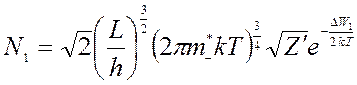
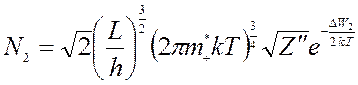Лекция №16

Электропроводность полупроводников

Полупроводники занимают особое место в группе металлов, проводников и диэлектриков. Их особенностью является величина электропроводности.

Для металлов: s = 10⁶ – 10⁷ Ом^-1м^-1;

для диэлектриков: s = 10^-12 – 10^-13 Ом^-1м^-1;

для полупроводников: s = 10⁴ – 10^-8 Ом^-1м^-1.

Электропроводность полупроводников изменяется на 12 порядков. По электропроводности они занимают особое положение между металлами и диэлектриками. Механизм электропроводности полупроводников значительно отличается от электропроводности металлов. Основной причиной является зависимость концентрации от температуры. У металлов с ростом температуры электропроводность уменьшается, а у полупроводников – увеличивается.

Другая особенность полупроводников – зависимость электропроводности от напряженности электрического поля.

Объяснения можно получить, рассматривая процессы в рамках зонной теории. У полупроводников сопротивление с переходом "зона – зона" или "примесный уровень – зона", то есть проводимость связана с возбуждением электронной системы.

У металлов концентрация свободных электронов велика, следовательно, нет необходимости возбуждать систему. С ростом температуры возникают проблемы, связанные с тем, что перенос осуществляется в периодической структуре, которая при поглощении внешней энергии переходит в возбужденное состояние в виде увеличения амплитуды колебаний узлов кристаллической решетки.