![]() , значит наложение дополнительного ограничения в виде
условия Борна-Кармано приведёт к тому, что аргумент функции должен изменяться
дискретно, то есть
, значит наложение дополнительного ограничения в виде
условия Борна-Кармано приведёт к тому, что аргумент функции должен изменяться
дискретно, то есть
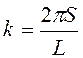 ,
,
L = Nc.
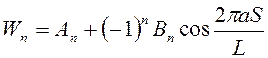 -
конечный вид модели зонной структуры твёрдого тела с учётом
периодичности внутренней структуры и характеристики потенциального барьера.
Таким образом, модель используется для истолкования свойств твёрдого тела.
-
конечный вид модели зонной структуры твёрдого тела с учётом
периодичности внутренней структуры и характеристики потенциального барьера.
Таким образом, модель используется для истолкования свойств твёрдого тела.
Пусть S = 0, тогда ![]() ,
,
S = 1 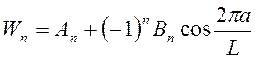 ,
,
S = 2 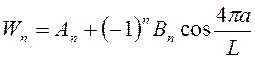 ,
,
S = 3 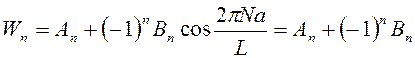 .
.
Вывод: в составе любой чётной или нечётной зоны число энергетических уровней равно числу атомов в кристаллической структуре длиной L.
По мере увеличения номера зоны её ширина становится больше, а количество энергетических уровней в ней остаётся неизменным, следовательно, расстояние между соседними энергетическими уровнями возрастает и вероятность перехода с одного уровня на другой уменьшается.
![]()
![]() , то есть
, то есть
![]()
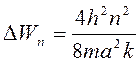 .
.
Энергетические уровни в трёхмерном кристалле
При переходе к трёхмерной структуре твёрдого тела сохраняется основное положение – число энергетических уровней в зоне будет равно числу атомов в элементарном объёме. Сохраняется общая закономерность увеличения ширины зоны по мере увеличения номера, но появляются особенности. Характеристики зон, рассматриваемые по отдельным направлениям, будут отличаться вследствие изменения постоянной решётки по этим направлениям. В результате в трёхмерном пространстве волнового вектора границы зон образуют сложные поверхности, называемые зонами Бриллюэна таким образом, что при различных направлениях волнового вектора расстояния между поверхностями могут существенно изменяться.
Для кодирования данных направлений разработана специальная система «Индексы Миллера».
Характеристики волновых функций для трёхмерных структур получаются как результат перемножения волновых функций по каждому направлению.
Для определения пространственного положения микрочастицы в структуре, пользуются понятием волновой функции, а для скорости – понятием групповой скорости волнового пакета. Групповая скорость пакета равна средней скорости движения частицы:
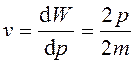 ;
;
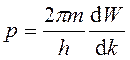 .
.
Лекция №11
Проводники, диэлектрики и полупроводники
Необходимо получить количественные оценки различий между тремя видами твердого тела, которые называются проводниками, диэлектриками и полупроводниками.
 Проводимость – это
способность проводить электрический ток. Нам необходимо определить условие для
свободного перемещения носителей заряда по структуре твёрдого тела. Если такие
условия существуют, то созданы предпосылки для переноса заряда, то есть для
протекания электрического тока. Если перемещение носителей невозможно, то
электрический ток отсутствует. Классические представления о переносе заряда
строятся на некоторых предпосылках. Пусть энергетическая структура твёрдого
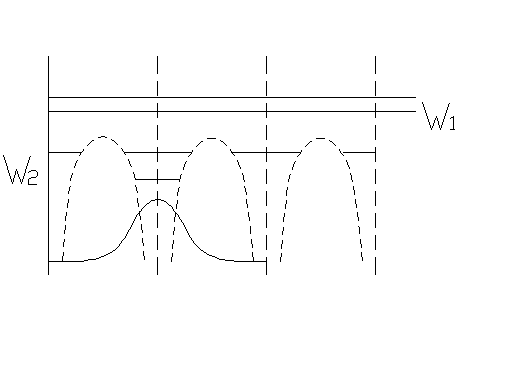
тела представлена следующим образом:
Проводимость – это
способность проводить электрический ток. Нам необходимо определить условие для
свободного перемещения носителей заряда по структуре твёрдого тела. Если такие
условия существуют, то созданы предпосылки для переноса заряда, то есть для
протекания электрического тока. Если перемещение носителей невозможно, то
электрический ток отсутствует. Классические представления о переносе заряда
строятся на некоторых предпосылках. Пусть энергетическая структура твёрдого
тела представлена следующим образом:
Если кинетическая энергия W1 превышает высоту потенциального барьера, то такой электрон может перемещаться из одной ячейки в другую – свободный электрон. Если энергия равна W2, то электрон локализован, то есть не может участвовать в процессе переноса заряда, значит, электрический ток отсутствует, но не исключено, что за счёт внешнего электрического поля электрон приобретёт энергию, достаточную для того, чтобы электрон превратился в свободный (поднялся над барьером). Для этого напряжённость поля должна быть такая, чтобы энергия поля позволила электрону перейти в свободное состояние.
Квантовая теория говорит о том, что местоположение электрона в структуре твёрдого тела определяется вероятностным путём через квадрат модуля волновой функции. Волновая функция является быстроубывающей по координате, но никогда не обращается в ноль. По мере удаления электрона от узла его связь ослабевает, а вероятность убывает. Следовательно, квантовая теория не исключает возможности нахождения электрона за пределами потенциального ящика (барьера). Вероятность нахождения электрона определяется высотой и шириной барьера. Чем больше характеристика K, тем меньше вероятность нахождения частицы за пределами барьера.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.