Получение навыков количественных оценок эффектов и явлений в структуре полупроводников и интегральных микросхем, страница 17

Будем считать, что электроны проводимости в полупроводниках распространяются кристалла также, как и свободные электроны в результате того, что мы приписываем им эффективную массу. Необходимо определить плотность тока. По второму закону Ньютона:

где f – сила,

w - ускорение,

m – масса.

Если частица находится в поле:

, где е – заряд электрона,

Е – напряженность поля.

Пусть средняя скорость частицы:

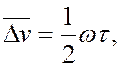
где t - время между двумя соударениями,

w - ускорение.

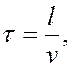
где l – расстояние, пройденное между двумя соударениями,

v – скорость теплового движения частиц.

Тогда получим:

 -

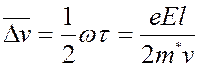- средняя скорость направленного движения электронов.

Плотность тока:

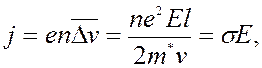
где n – концентрация носителей,

s - электропроводность материала.

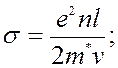
с другой стороны

где

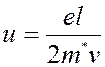 - подвижность носителей.

Подвижность – это характеристика скорости направленного движения носителей под воздействием электрического поля.

Встаёт вопрос: почему не развивается процесс лавинного увеличения электрического тока?

Этого не происходит потому, что кристалл не является идеальным.

В идеальном кристалле носители заряда не испытывают противодействия со стороны кристаллической решетки, следовательно, условия существования частицы в одной ячейке будут такие же, как и в другой. Это означает, что в результате действия механизма туннельного переноса любая частица с равной вероятностью может находится в любой точке пространства, то есть носители могут перемещаться по всему кристаллу, то есть участвовать в образовании электрического тока. Отличие реальных кристаллических структур от идеальных проявляется в том, что существуют препятствующие переносу заряда явления: дефекты в виде искажений кристаллической решетки. Эффекты взаимодействия частиц с колеблющимися узлами обозначаются понятием рассеяния на фононах. Другой причиной, препятствующей протеканию тока, является наличие инородных атомов в структуре.

В итоге устанавливается некое динамическое равновесие. Внешним проявлением этого равновесия является неизменный электрический ток, протекающий через образец.

Волновое представление процессов переноса заряда

в полупроводниках

Любое движение  частицы может быть представлено волновым процессом с длиной волны l:

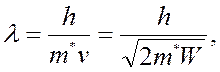
где W – энергия.

То есть, если протекает электрический ток, то в структуре твердого тела распространяется электромагнитное поле.

Лекция №17

Электропроводность полупроводников

Электропроводность зависит от температуры.

s = enu, следовательно, s(T) = en(T)u(T), подвижность зависит от температуры по сложному закону. При низких температурах подвижность оказывается:

u ~ T^3/2.

Это означает, что растёт L – длина пробега, так как возрастает скорость пеплового движения. По мере увеличения температуры растет энергия, амплитуда и частота колебаний узлов решетки. Это снижает возможность для переноса носителей, то есть увеличивает вероятность рассеяния на узлах решетки. В этом интервале температур:

 

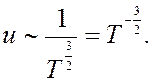
В то же время известно, что с ростом температуры проводимость у полупроводников всегда возрастает. Следовательно, определяющим фактором для электропроводности является температурная зависимость – концентрация электронов в беспримесном полупроводнике:

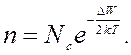
В случае примесного полупроводника:

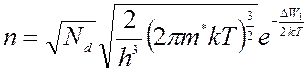
или

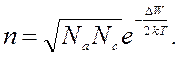
Из формулы видно, что по мере увеличения температуры степень уменьшается - концентрация возрастает.

Освобождение примесного уровня означает, что экспоненциальный множитель приближается к единице, и мы можем считать, что при ΔW << kT происходит истощение донорного уровня. Это происходит до тех пор, пока     ΔW ≈ kT, когда начинается переход из валентной зоны в зону проводимости и концентрация снова возрастает.

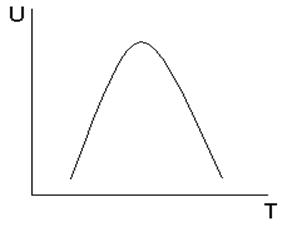
Сопоставим экспоненциальный множитель  с другим экспоненциальным множителем . Концентрация электронов, перешедших из валентной зоны в зону проводимости, от температуры отличается от аналогичной зависимости для примесных уровней большей крутизной. В результате всех рассуждений получим графическую интерпретацию: