Важнейшим следствием упрощений, принятых в теории Зоммерфельда, является возможность решения задачи в одноэлектронном приближении, то есть для каждого электрона решение будет одинаковым. Это позволяет вместо решения множества уравнений Шредингера воспользоваться решением для одного электрона. Решение основной квантово-механической задачи сводится к нахождению решения уравнения Шредингера для одного электрона в одномерном приближении.
 |
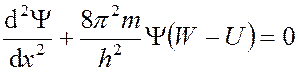
юдним из важных упрощений теории Зоммерфельда является предположение о возможности представления потенциального ящика с вертикальными стенками, основание которого получено совмещением дна этого ящика с уровнем нулевой энергии, то есть значение потенциальной энергии также нулевое, то есть:
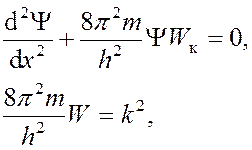
тогда волновой вектор:
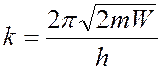, уравнение Шредингера:
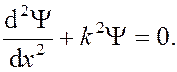
Для решения линейных дифференциальных уравнений в частных производных необходимо сформулировать граничные условия.
Граничные условия должны отражать положение потенциального ящика.
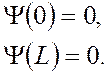
Выполнение первого граничного условия (
) потребует, чтобы решение имело вид:
.
Учет второго граничного условия требует, чтобы функция синуса обращалась в 0:
kx = 0, если 
,
kL = Sn, где S = 1, 2, 3…
Решение уравнения Шредингера имеет вид:
При S =1 При S = 2
 |
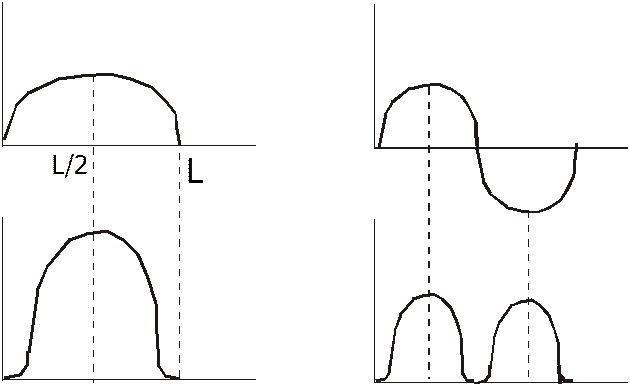Увеличение S сопровождается возрастанием кинетической энергии частицы, а значит, и возрастанием скорости частицы в пространстве. То есть для быстро движущихся частиц становятся более вероятными значения x, характеризующие её положение в данный момент времени.
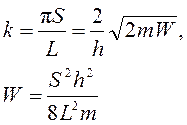
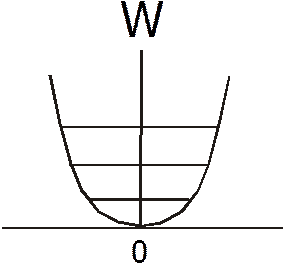
Кинетическая энергия частицы в потенциальном ящике может принимать только дискретные значения, зависящие от квантового числа S. В энергетической интерпретации:
 |
В теории Зоммерфельда L может рассматриваться как величина неограниченная.
Лекция №5
Условие Борна-Кармано
Результаты теории Зоммерфельда удалось получить, переходя к волновому процессу, когда на длине L должно укладываться целочисленное значение полуволн так, чтобы на границах потенциального ящика значение волновой функции обращалось в 0. В соответствии с положениями Борна-Кармано на волновую функцию было наложено ещё одно ограничение: бесконечный кристалл представляется в таком виде, что каждый атом смещается по оси по отношению к другому (L замыкается в кольцо).
Это означает, что Ni атом должен совмещаться с N+Ni атомом.
Тогда условие периодичности имеет вид:
где n – число витков.
Иными словами, потребовали, чтобы функция была периодичной. В конечном итоге условие Борна-Кармано требует совпадения волновых функций, отстоящих на период (за период берется конечный размер кристалла – L). Если такое требование выполняется, то из решения уравнения Шредингера вытекает следующая модель для разрешенных значений энергии частицы, находящейся в пределах кристалла:
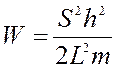
, где S = 1, 2, 3… -
квантовое число.
Пусть расстояние между двумя разрешенными значениями
энергии 
. Рассмотрим уровни S иS+1:
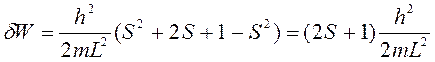, где L –
размер кристалла.
Эта модель определяет расстояние между разрешенными уровнями энергии.
Возьмем в качестве критерия величину kT – значение энергии движущейся частицы, находящейся в
тепловом равновесии со средой. Если kT > 
, то за счет теплового взаимодействия
частица может подняться с одного уровня на другой, если же kT
< , то переход практически невозможен.
Например, при L=10-8 см - >> kT;
при увеличении же размера до L=10-1 см
- < kT.
То есть в рамках упрощенной теории появляются выводы, определяющие фундаментальные свойства твердого тела, в частности металлов.
Волновая функция трехмерного кристалла
В рамках теории Зоммерфельда оказывается возможным представить волновую функцию в трехмерного кристалла как произведение волновых функций по каждому направлению, то есть вероятностную оценку нахождения микрочастицы с известной энергией в каждой точке трехмерного пространства 1при рассмотрении как ограниченных так и неограниченных размеров кристалла. Из этого факта вытекает, что значение энергий частиц можно представить, как сумму значений энергий, находимых по уравнению Шредингера по каждому направлению:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.