Основные электрические параметры антенн. Эффективная площадь антенны А, страница 9

Рассмотрим несколько примеров.

1. Коэффициент направленного действия элементарного диполя.

Как известно, ДН элементарного диполя выражается формулой . При этом

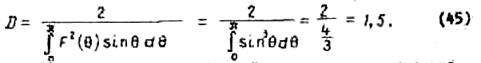
2. Коэффициент направленного действия полуволнового вибратора.

ДН полуволнового вибратора

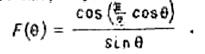
Поэтому его коэффициент направленного действия

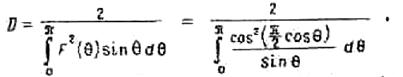
Интеграл в последнем выражении вычисляется приближенно с помощью специальных функций или графическим путем. Его численное значение равно 1,22. Поэтому

Тема 3

ПРИЕМНЫЕ АНТЕННЫ

Задача приемной антенны состоит в том, чтобы извлечь энергию из приходящего к ней полезного сигнала и передать ее на вход приемника.

В ряде случаев удобно представить приемную антенну как некоторый эквивалентный генератор, нагрузкой которого является вход приемника. При таком представлении необходимо:

а) найти величину э.д.с., наводимой в антенне, при заданной напряженности поля в точке приема;

б) определить зависимость этой э.д.с. от направления прихода электромагнитной волны, ее поляризации и частоты принимаемого сигнала;

в) найти величину сопротивления антенны, выполняющего роль внутреннего сопротивления генератора и зависимость его от частоты;

г) определить мощность, отдаваемую антенной приемнику и условия передачи максимальной мощности.

Известно два принципиально различных способа исследования приемных антенн.

1. Приемная антенна разбивается на элементы, длина которых значительно меньше длины волны. В каждом таком элементе наводится э.д.с. с соответствующей фазой. Путем интегрирования э.д.с., наводимых во всех элементах, определяется э.д.с. на зажимах антенны, а затем и все остальные параметры приемной антенны. Этот метод называется методом наводимых э.д.с. Он чрезвычайно сложен и применяется крайне редко.

2. В основе другого метода лежит принцип взаимности, строго доказанный для антенн М.П. Свешниковой в 1927 г. и использованный для исследования приемных антенн М.С. Нейманом в 1935 г. Остановимся на принципе взаимности более подробно.

ПРИМЕНЕНИЕ ПРИНЦИПА ВЗАИМНОСТИ ДЛЯ АНАЛИЗА СВОЙСТВ ПРИЕМНЫХ АНТЕНН

В безграничном пространстве, заполненном изотропной линейной средой, параметры которой не зависят ни от направления, ни от амплитуды векторов напряженности поля  и  , но могут меняться скачком на конечном числе поверхностей, расположены антенны , и , произвольным образом ориентированные друг относительно друга.

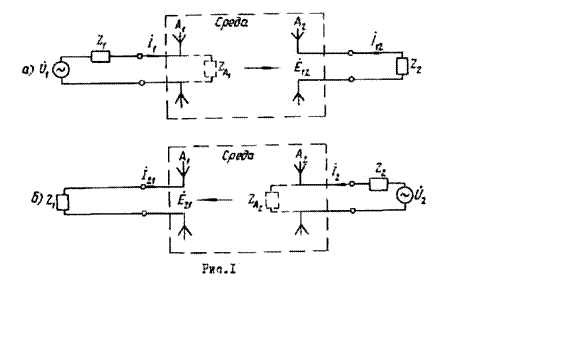Рис.1,а соответствует распространению электромагнитных волн слева направо (антенна , является передающей, а антенна  - приемной), а на рис.1,6 антенна , является приемной, а антенна - передающей.

Если в цепи антенны  действует э.д.с.  и она вызывает в цепи антенны  ток  (рис.1,а), то на основании принципа взаимности можно утверждать, что под влиянием э.д.с. , действующей в цепи антенны , в цепи антенны , появится такой ток  (рис.1,б), что справедливым будет соотношение

Проведем несложные рассуждения.

Пусть антенна  работает в режиме передачи, а антенна - в режиме приема. Под влиянием э.д.с.  в цепи антенны , потечет ток

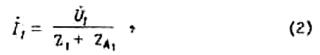
где      - сопротивление, включенное в цепь антенны ;

 - входное сопротивление антенны , в режиме передачи.                                                           

При этом в окружающем пространстве возникнет электромагнитное поле.

Если через  обозначить расстояние между антеннами, то напряженность электрического поля около антенны

где       - действующая длина антенны ;

 - значение нормированной ДН антенны , в направлении антенны .

Подставляя значение  из выражения (2) в (3), после простых преобразований получаем

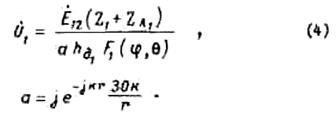
Если в качестве передающей используется антенна , а роль приемной выполняет антенна , то, проводя аналогичные рассуждения, можно записать

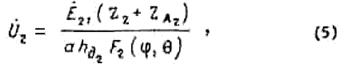
где     - э.д.с., включенная в цепь антенны ;

 - действующая длина антенны ;

 - значение нормированной ДН антенны  в направлении антенны;       

- напряженность поля, возбуждаемого, антенной  у антенны ;