Идея простейших щелевых антенн принадлежит советским ученик М.А. Бонч-Бруевичу и М.С. Нейману. Профессор Бонч-Бруевич предложил в качестве остронаправленной антенны использовать ряд щелей в наружной оболочке коаксиального кабеля, а профессор Нейман в 1940 г. предложил излучатели в виде малых круглых или прямолинейных щелей на поверхности объемного резонатора.
Теория щелевых антенн была разработана советскими учеными А.А. Пистолькорсом и Я.Н. Фельдом.
Большой заслугой Пистолькорса явились его работы, связанные с применением принципа двойственности к теории и расчету щелевых антенн (1944г.). На их основе можно анализировать щелевые антенны путем обобщения теории проволочных (линейных) антенн. Если щель прорезана в плоском металлическом экране достаточно больших размеров, то вопрос о расчете такой антенны легко решается на основе принципа двойственности.
ПРИМЕНЕНИЕ ПРИНЦИПА ДВОЙСТВЕННОСТИ ДЛЯ АНАЛИЗА СВОЙСТВ ЩЕЛЕВЫХ АНТЕНН
Принцип двойственности вытекает из симметрии уравнений Максвелла в отношении электрического и магнитного попей. Применительно к антеннам он может быть сформулирован следующим образом:
решение уравнений Максвелла для
электрического поля при заданных в отношении этого поля граничных условиях
справедливо также и для магнитного поля при тех же граничных условиях,
принятых в отношении магнитного поля. Это означает, что если в решении,
например, для электрического поля ![]() сделать перестановки
вида
сделать перестановки
вида ![]() ,
, ![]() ,
, ![]() , то автоматически будет записано решение
для магнитного поля.
, то автоматически будет записано решение
для магнитного поля.
Принцип двойственности, строго говоря, можно использовать для исследования щелевых антенн только идеализированного типа в виде щелей на безграничной бесконечно тонкой идеально проводящей плоскости. Электромагнитное поле такой щелевой антенны сравнивается с полем соответствующего металлического аналога в виде бесконечно тонкой металлической пластины, форма и размеры которой совпадают с формой и размерами щели. При соблюдении одинаковых граничных условий для электрического поля щелевой антенны и магнитного поля металлического аналога по известному полю во внешнем пространстве металлической антенны можно легко найти поле щелевой антенны. Эквивалентность электрического и магнитного полей щели и ее металлического аналога обусловливает их одинаковое направленное действие.
При исследовании поля
прямолинейной щели воспользуемся известными нам выражениями для поля
симметричного вибратора. Если симметричный вибратор (металлический аналог
щелевой антенны) помещен в начало координат и ось его совпадает с направлением
оси ![]() , то в дальней зоне, как известно,
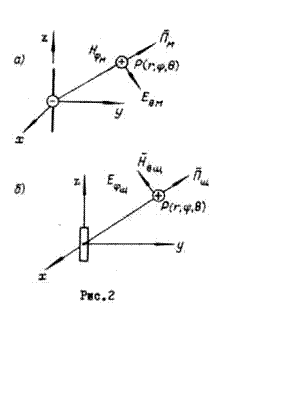
возбуждается электромагнитное поле (рис.2,а), характеризуется выражениями:
, то в дальней зоне, как известно,
возбуждается электромагнитное поле (рис.2,а), характеризуется выражениями:
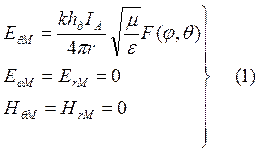
где символ ![]() означает, что написаны
составляющие поля металлического аналога.
означает, что написаны
составляющие поля металлического аналога.
Для того чтобы можно было воспользоваться перестановками в соответствии с принципом двойственности, преобразуем соотношения (1), пользуясь формулой
![]()
где ![]() - магнитное поле у
поверхности металлического аналога. После такой замены формулы (1) приобретают
вид
- магнитное поле у
поверхности металлического аналога. После такой замены формулы (1) приобретают
вид
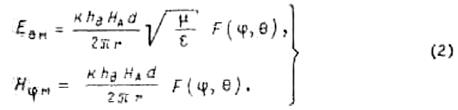
Произведя необходимые замены в соответствии с принципом двойственности, для поля таким же образом ориентированной щелевой антенны (рис.2,б) получим
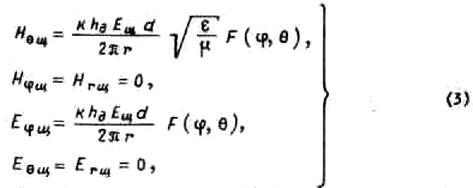
где ![]() - напряженность поля
между стенками щели в центральном ее сечении.
- напряженность поля
между стенками щели в центральном ее сечении.
После несложных преобразований можно записать следующие выражения дня электрического поля металлического аналога:
![]()
а для электрического поля щели:
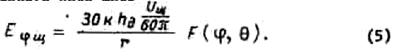
В последнем выражении использовано соотношение![]() .
.
Из сравнения щелевой антенны и ее металлического аналога можно сделать следующие выводы.
1. Диаграммы направленности щели и ее металлического аналога совпадают.
2. Действующая длина щелевой антенны равна действующей длине ее металлического аналога.
3. При замене щели
металлическим аналогом напряженность поля в той же точке пространства
сохраняется неизменной по величине, если напряжение на щели и ток в
металлическом аналоге связаны соотношением ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.