Основные электрические параметры антенн. Эффективная площадь антенны А, страница 42

Для синфазного сложения полей соседних витков в направлении оси спирали должно выполняться условие

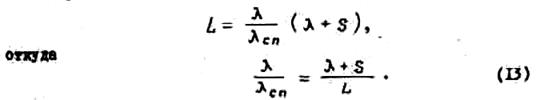
Таким образом, после несложного преобразования получаем, что

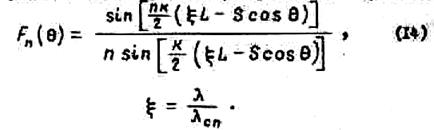
Оценку   параметров   цилиндрических   спиралей   и   выбор размеров   удобно   производить   при   помощи   полуэмпирических   формул:

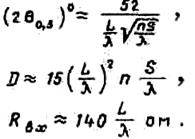
П р и меч а н и е.    Формулы   справедливы для спиралей с числом витков      и   при углах   подъема  от 12° до 16°.

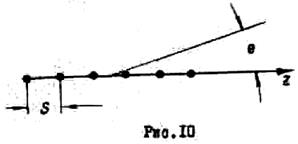
При приближенных расчетах длину витка L выбирают равной расчетной длине волны , шаг спирали S - в пределах (0,150,3), а коэффициент укорочения волны   = 1,25.

Рабочий диапазон определяется из условия:  

Диаметр экрана выбирается в пределах (1,0 * 1,6) I , где l - длина спирали.

К достоинствам цилиндрических спиральных антенн следует отнсти простоту конструкции и широкую диапазонность (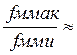1,7).

Недостатком является невозможность формирования при помощи одной спирали ДН шириной менее 25° (число витков нельзя брать больше II).

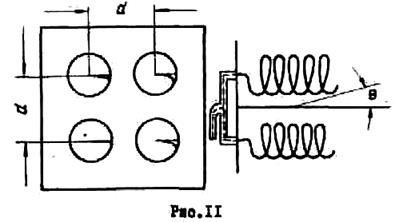
Для обострения ДН применяют решетки из нескольких идентичных спиралей. На рис.11 показана решетка из 4 спиралей, предназначенная для обострения ДН в двух главных плоскостях. Диаграмма направленности ее в горизонтальной или вертикальной плоскости определяется выражением

,где - ДН одиночной спирали в рассматриваемой плоскости;

d - расстояние между центрами спиралей; .

- угол, отсчитываемый от оси спирали в рассматриваемой плоскости.

Логарифмические спиральные антенны. Такие антенны относятся к разряду частотно-независимых (сверхширокополосных) антенн, коэффициент перекрытия которых может достигать 10, 20 и более. Построение частотно-независимых антенн основано на принципе электродинамического подобия: при одновременном изменении длины волны и всех геометрических размеров в .одинаковой пропорции основные электрические характеристики антенны остаются неизменными. Во всех частотно-независимых антеннах на определенной длине волны Е излучении участвует только часть антенны, активная ее область. При изменении длины волны эта область перемещается вдоль антенны, не меняя своих относительных размеров. Одной из разновидностей частотно-независимых антенн является равноугольная логарифмическая спиральная антенна. Принцип ее работы основан на том, что если излучающая структура полностью определяется полярными углами, то отношение линейных размеров излучателя к длине волны остается постоянным, а ДН не зависит от частоты.

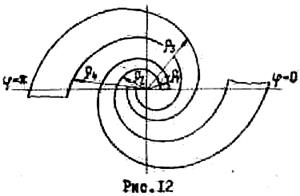
Равноугольная логарифмическая спираль строится в полярных координатах в соответствии с уравнением

где   г₀- радиус-вектор в начале спирали (при = 0);

а - постоянный коэффициент.

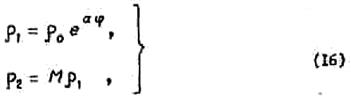
Двухзаходная спираль (рис.12) образована двумя проводниками или щелями, ширина которых возрастает с ростом угла . Уравнения, определяющие границы первого проводника, могут быть записаны в виде

а второго -

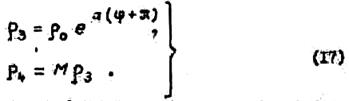
В случае оптимальной антенны (когда часть плоскости, заполненная металлом, равна свободной части плоскости):  а = 0,3; П = 0,62.

При увеличении угла  на  (один полный оборот) радиус-вектор р возрастает в е  раз. Это свидетельствует о том, что каждый последующий виток имеет размеры в   раз большие, чем предыдущий.                                                                           

Если за единицу длины взять длину волны, а через р` обозначить радиус-вектор, измеренный в долях волны, то

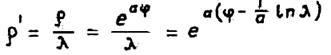
или

где

Реальная антенна имеет конечную длину, но тем не менее она эффективно работает в очень широком диапазоне волн от  до .При этом величина ЛЛТОКС

определяется длиной спирали, а — размерами узла питания.

Логарифмическая спираль работает в режиме бегущих волн. Вследствие интенсивного излучения амплитуда тока быстро затухает: на отрезке длиною   амплитуда убывает примерно в 100 раз.

Входное сопротивление логарифмической спирали Zвх (если она равноугольная).